Bài 18 trang 31 SBT Toán 10 Cánh Diều là một bài tập quan trọng trong chương trình học Toán 10, tập trung vào việc rèn luyện kỹ năng về vectơ và các phép toán vectơ. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các bài toán thực tế, giúp củng cố và nâng cao hiểu biết về vectơ.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 18 trang 31 SBT Toán 10 Cánh Diều, giúp các em học sinh tự tin hơn trong quá trình học tập và ôn luyện.
Anh Trung có kế hoạch đầu tư 400 triệu đồng vào hai khoản X và Y. Để đạt được lợi nhuận thì khoản X phải đầu tư ít nhất 100 triệu đồng và số tiền đầu tư cho khoản Y không nhỏ hơn số tiền cho khoản X
Đề bài
Anh Trung có kế hoạch đầu tư 400 triệu đồng vào hai khoản X và Y. Để đạt được lợi nhuận thì khoản X phải đầu tư ít nhất 100 triệu đồng và số tiền đầu tư cho khoản Y không nhỏ hơn số tiền cho khoản X. Viết hệ bất phương trình bậc nhất hai ẩn để mô tả hai khoản đầu tư đó và biểu diễn miền nghiệm của hệ bất phương trình vừa tìm được.
Phương pháp giải - Xem chi tiết
- Gọi x, y lần lượt là số tiền anh Trung đầu tư vào khoản X và Y
- Biểu diễn hai khoản đầu tư theo x, y
- Sử dụng dữ liệu đề bài cho để lập hệ bất phương trình ẩn x, y
- Xác định miền nghiệm của bất phương trình trên mặt phẳng tọa độ
Lời giải chi tiết
Gọi x, y (triệu đồng) lần lượt là số tiền anh Trung đầu tư vào khoản X và Y. (\(x,y \ge 0\))
Vì anh Trung đầu tư 400 triệu đồng vào hai tài khoản X và Y nên ta có \(x + y \le 400\)
Để đạt được lợi nhuận thì khoản X phải đầu tư ít nhất 100 triệu đồng nên ta có \(x \ge 100\).
Số tiền đầu tư cho khoản Y không nhỏ hơn số tiền cho X nên ta có \(y \ge x\) hay \(x - y \le 0\)
Từ đó ta có hệ bất phương trình: \(\left\{ {\begin{array}{*{20}{c}}{x + y \le 400}\\{x \ge 100}\\{x - y \le 0}\end{array}} \right.\)
Ta vẽ bốn đường thẳng:
\({d_1}\): x + y = 400 là đường thẳng đi qua hai điểm có tọa độ (400;0) và (0;400);
\({d_2}\): x = 100 là đường thẳng song song với trục Oy và đi qua điểm có tọa độ (100;0);
\({d_3}\): x – y = 0 là đường thẳng đi qua hai điểm có tọa độ (0;0) và (1;1).
Ta xác định từng miền nghiệm của từng bất phương trình trong hệ, gạch đi các phần không thuộc miền nghiệm của mỗi bất phương trình.
Miền nghiệm của hệ bất phương trình là miền trong tứ giác ABC với như hình vẽ sau:
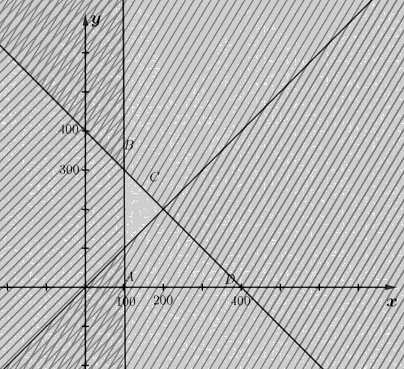
Trong đó A(100;100), B(100;300) và C(200;200)
Bài 18 trang 31 SBT Toán 10 Cánh Diều thuộc chương trình học Toán 10, tập trung vào việc ứng dụng các kiến thức về vectơ trong không gian để giải quyết các bài toán hình học. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản về vectơ, bao gồm:
Bài 18 trang 31 SBT Toán 10 Cánh Diều thường bao gồm các dạng bài tập sau:
Để giúp các em học sinh hiểu rõ hơn về cách giải bài tập này, chúng ta sẽ đi vào giải chi tiết từng phần của bài 18 trang 31 SBT Toán 10 Cánh Diều. (Nội dung giải chi tiết sẽ được trình bày ở đây, bao gồm các bước giải, giải thích rõ ràng và các lưu ý quan trọng. Ví dụ:)
Giải:
Vectơ AB có tọa độ là: AB = (4 - 1; 5 - 2; 6 - 3) = (3; 3; 3)
Vậy, tọa độ của vectơ AB là (3; 3; 3).
Để giải các bài tập về vectơ một cách nhanh chóng và hiệu quả, các em học sinh có thể áp dụng một số mẹo sau:
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập về vectơ, các em học sinh có thể tham khảo một số bài tập tương tự sau:
Bài 18 trang 31 SBT Toán 10 Cánh Diều là một bài tập quan trọng giúp các em học sinh củng cố kiến thức về vectơ và các phép toán vectơ. Hy vọng với lời giải chi tiết và các mẹo giải nhanh mà Giaitoan.edu.vn cung cấp, các em sẽ tự tin hơn trong quá trình học tập và ôn luyện môn Toán 10.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục tri thức. Chúc các em học tập tốt!