Bài 16 trang 79 SBT Toán 10 Cánh Diều là một bài tập quan trọng trong chương trình học Toán 10, tập trung vào việc rèn luyện kỹ năng về vectơ và các phép toán vectơ. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các bài toán thực tế, giúp củng cố và nâng cao hiểu biết về vectơ.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 16 trang 79 SBT Toán 10 Cánh Diều, giúp các em học sinh tự tin hơn trong quá trình học tập và ôn luyện.
Gia đình bạn An sở hữu một mảnh đất hình tam giác. Chiều dài của hàng rào MN là 150 m, chiều dài của hàng rào MP là 230 m
Đề bài
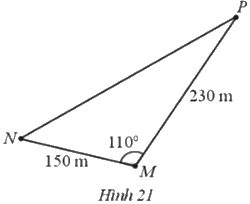
Gia đình bạn An sở hữu một mảnh đất hình tam giác. Chiều dài của hàng rào MN là 150 m, chiều dài của hàng rào MP là 230 m. Góc giữa hai hàng rào MN và MP là 1100 (Hình 21)
a) Diện tích mảnh đất mà gia đình bạn An sở hữu là bao nhiêu mét vuông (làm tròn kết quả đến hàng phần mười)?
b) Chiều dài hàng rào NP là bao nhiêu mét (làm tròn kết quả đến hàng phần mười)?
Phương pháp giải - Xem chi tiết
Bước 1: Sử dụng công thức diện tích \(S = \frac{1}{2}MN.MP\sin M\) để tính diện tích ∆MNP
Bước 2: Sử dụng định lí cosin để tính độ dài NP
Bước 3: Kết luận
Lời giải chi tiết
a)\({S_{MNP}} = \frac{1}{2}MN.MP\sin M = \frac{1}{2}.150.230.\sin {110^0} \approx 16209,7\) (m2)
Vậy diện tích mảnh đất mà gia đình bạn An sở hữu là 16209,7 m2
b) Áp dụng định lí cosin cho ∆ABC ta có: \(N{P^2} = M{N^2} + M{P^2} - 2.MN.MP.\cos M\)
\( \Rightarrow NP = \sqrt {M{N^2} + M{P^2} - 2.MN.MP.\cos M} \)\( = \sqrt {{{150}^2} + {{230}^2} - 2.150.230.\cos {{110}^0}} \approx 314,6\)(m)
Vậy chiều dài hàng rào NP là 314,6 m
Bài 16 trang 79 SBT Toán 10 Cánh Diều thuộc chương trình học về vectơ trong không gian. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản về vectơ, bao gồm:
Bài 16 trang 79 SBT Toán 10 Cánh Diều thường bao gồm các dạng bài tập sau:
Để giúp các em học sinh hiểu rõ hơn về cách giải bài tập này, chúng ta sẽ đi vào giải chi tiết từng phần của bài 16 trang 79 SBT Toán 10 Cánh Diều. (Nội dung giải chi tiết sẽ được trình bày ở đây, bao gồm các bước giải, công thức sử dụng và giải thích rõ ràng từng bước. Ví dụ:)
Giải:
Vectơ AB được tính bằng hiệu tọa độ của điểm B trừ đi tọa độ của điểm A:
AB = (4 - 1; 5 - 2; 6 - 3) = (3; 3; 3)
Vậy, tọa độ của vectơ AB là (3; 3; 3).
Để giải các bài tập về vectơ một cách nhanh chóng và chính xác, các em học sinh có thể tham khảo một số mẹo sau:
Ngoài sách giáo khoa và sách bài tập, các em học sinh có thể tham khảo thêm các tài liệu sau để học tốt môn Toán 10:
Bài 16 trang 79 SBT Toán 10 Cánh Diều là một bài tập quan trọng giúp các em học sinh củng cố kiến thức về vectơ. Hy vọng với lời giải chi tiết và các mẹo giải bài tập mà Giaitoan.edu.vn đã cung cấp, các em sẽ tự tin hơn trong quá trình học tập và đạt kết quả tốt nhất.