Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong sách bài tập Toán 10 Cánh Diều. Bài viết này sẽ hướng dẫn bạn từng bước giải bài 29 trang 32, giúp bạn hiểu rõ bản chất của bài toán và áp dụng kiến thức vào các bài tập tương tự.
Chúng tôi luôn cố gắng cung cấp nội dung chất lượng cao, chính xác và cập nhật nhất để hỗ trợ bạn trong quá trình học tập môn Toán.
Một xưởng sản xuất bàn và ghế. Một chiếc bàn cần 1,5 giờ lắp ráp và 1 giờ để hoàn thiện; một chiếc ghế cần 1 giờ để lắp ráp và 2 giờ để hoàn thiện.
Đề bài
Một xưởng sản xuất bàn và ghế. Một chiếc bàn cần 1,5 giờ lắp ráp và 1 giờ để hoàn thiện; một chiếc ghế cần 1 giờ để lắp ráp và 2 giờ để hoàn thiện. Bộ phận lắp ráp có 3 nhân công, bộ phận hoàn thiện có 4 nhân công. Biết thị trường luôn tiêu thụ hết sản phẩm của xưởng và lượng ghế tiêu thụ không vượt quá 3,5 lần số bàn.
a) Viết hệ bất phương trình mô tả số lượng bàn và ghế mà trong một ngày phân xưởng có thể sản xuất, biết một nhân công làm việc không quá 8 tiếng mỗi ngày.
b) Biểu diễn miền nghiệm của hệ bất phương trình đó.
c) Biết một chiếc bàn lãi 600 nghìn đồng, một chiếc ghế lãi 450 nghìn đồng. Hỏi trong một ngày, xưởng cần sản xuất bao nhiêu chiếc bàn, bao nhiêu chiếc ghế để thu được tiền lãi cao nhất.
Lời giải chi tiết
a) Gọi số bàn xưởng sản xuất được là x (bàn) và số ghế xưởng sản xuất được là y (ghế) (x, y ∈ ℕ).
Xưởng có 3 công nhân lắp ráp và một công nhân làm việc không quá 8 tiếng mỗi ngày nên tổng thời gian lắp ráp một ngày là 3.8 = 24 (giờ).
Xưởng có 4 công nhân hoàn thiện và một công nhân làm việc không quá 8 tiếng mỗi ngày nên tổng thời gian lắp ráp một ngày là: 4.8 =32 (giờ).
Tổng thời gian lắp ráp x chiếc bàn và y chiếc ghế không vượt quá 24 giờ nên \(1,5x + y \le 24\quad (1)\)
Tổng thời gian hoàn thiện x chiếc bàn và y chiếc ghế không vượt quá 32 giờ nên:
\(x + 2y \le 32\quad (2)\)
Vì lượng ghế tiêu thụ không vượt quá 3,5 lần số bàn nên \(3,5x \ge y{\rm{ }}\left( 3 \right)\)
Từ (1), (2), (3) và điều kiện của x, y nên ta có hệ bất phương trình sau:
\(\left\{ {\begin{array}{*{20}{c}}{1,5x + y \le 24}\\{x + 2y \le 32}\\{3,5x - y \ge 0}\\{x \ge 0}\\{y \ge 0}\end{array}} \right.\)
b) Vẽ các đường thẳng:
d1: 1,5x + y = 24 đi qua hai điểm (16; 0) và (0; 24).
d2: x + 2y = 32 đi qua hai điểm (32; 0) và (0; 16).
d3: 3,5x – y = 0 đi qua hai điểm (0; 0) và (2; 7).
d4: x = 0 là trục Oy.
d5: y = 0 là trục Ox.
Gạch đi các phần không thuộc miền nghiệm của từng bất phương trình.
Miền nghiệm của hệ bất phương trình là miền trong tứ giác OABC với O(0; 0), A(4; 14), B(8; 12), C(16; 0).
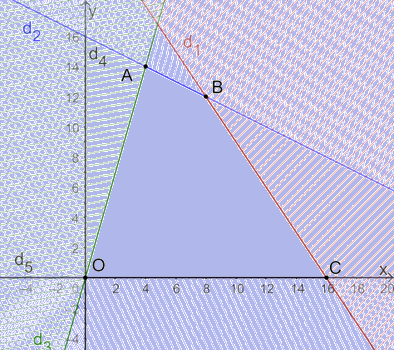
c) Số tiền lãi mà phân xưởng thu được khi bán x chiếc bàn và y chiếc ghế là: 600x + 450y (nghìn đồng).
Đặt F = 600x + 450y.
Thay x,y lần lượt là tọa độ các điểm O, A, B, C, D vào biểu thức F:
\(O(0;0)\) | \(A(4;14)\) | \(B(8;12)\) | \(C(16;0)\) | |
\(F = 600x + 450y\) | \(0\) | \(8700\) | \(10200\) | \(9600\) |
F đạt giá trị lớn nhất bằng 10200 tại \(x = 8,y = 12\)
Vậy xưởng cần sản xuất 8 chiếc bàn và 12 chiếc ghế để thu được tiền lãi lớn nhất là 10 200 000 đồng.
Bài 29 trang 32 SBT Toán 10 Cánh Diều thuộc chương trình học về vectơ trong mặt phẳng. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức về phép cộng, phép trừ vectơ, tích của một số với vectơ, và các tính chất của các phép toán này để giải quyết các bài toán liên quan đến hình học phẳng.
Bài 29 thường bao gồm các dạng bài tập sau:
Để giải bài 29 trang 32 SBT Toán 10 Cánh Diều một cách hiệu quả, bạn cần:
Dưới đây là lời giải chi tiết cho từng phần của bài 29 (ví dụ, giả sử bài 29 có 3 phần a, b, c):
Đề bài: Cho hai vectơ a và b. Tính a + b.
Lời giải: Để tính a + b, ta cộng các thành phần tương ứng của hai vectơ. Nếu a = (x1, y1) và b = (x2, y2) thì a + b = (x1 + x2, y1 + y2).
Đề bài: Chứng minh rằng a - b = - (b - a).
Lời giải: Ta có a - b = a + (-b). Mặt khác, b - a = b + (-a). Do đó, - (b - a) = - (b + (-a)) = -b + a = a - b. Vậy, a - b = - (b - a).
Đề bài: Cho điểm A(xA, yA) và vectơ u = (x, y). Tìm tọa độ điểm B sao cho AB = u.
Lời giải: Gọi tọa độ điểm B là (xB, yB). Ta có AB = (xB - xA, yB - yA). Để AB = u, ta cần có xB - xA = x và yB - yA = y. Từ đó, suy ra xB = xA + x và yB = yA + y. Vậy, tọa độ điểm B là (xA + x, yA + y).
Để củng cố kiến thức về vectơ, bạn có thể làm thêm các bài tập tương tự sau:
Bài 29 trang 32 SBT Toán 10 Cánh Diều là một bài tập quan trọng giúp bạn hiểu rõ hơn về các phép toán vectơ và ứng dụng của chúng trong hình học phẳng. Hy vọng với lời giải chi tiết và hướng dẫn trên, bạn sẽ giải quyết bài tập này một cách dễ dàng và hiệu quả.