Bài 50 trang 62 SBT Toán 10 Cánh Diều là một bài tập quan trọng trong chương trình học Toán 10. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức đã học về vectơ, phép toán vectơ, và các ứng dụng của vectơ trong hình học.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 50 trang 62 SBT Toán 10 Cánh Diều, giúp các em học sinh hiểu rõ bản chất bài toán và rèn luyện kỹ năng giải toán.
Vẽ đồ thị hàm số của mỗi hàm số sau:
Đề bài
Vẽ đồ thị hàm số của mỗi hàm số sau:
a) \(y = 2{x^2} - 8x + 1\)
b) \(y = - {x^2} + 4x - 3\)
Phương pháp giải - Xem chi tiết
Xác định đỉnh của parabol \(y = a{x^2} + bx + c\): \(\left( {\frac{{ - b}}{{2a}}; - \frac{\Delta }{{4a}}} \right)\) và trục đối xứng của đường thẳng \(x = - \frac{b}{{2a}}\)
Lời giải chi tiết
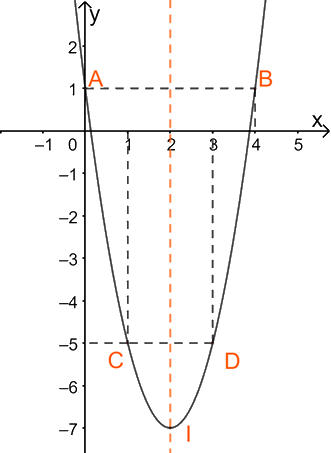
a) Hàm số \(y = 2{x^2} - 8x + 1\)có \(a = 2 > 0;b = - 8;c = 1\) và \( - \frac{b}{{2a}} = - \frac{{ - 8}}{{2.2}} = 2\)
+ Đỉnh của parabol là \(I\left( {2; - \frac{{{{\left( { - 8} \right)}^2} - 4.2.1}}{{4.2}}} \right) = \left( {2; - 7} \right)\)
+ Trục đối xứng \(x = 2\)
+ Giao điểm với trục tung là A(0;1)
+ Điểm đối xứng với A(0;1) qua trục đối xứng \(x = 2\) là B(4;1)
+ Lấy các điểm C(1; -5) và D(3;-5)
Từ đó ta có đồ thị hàm số:
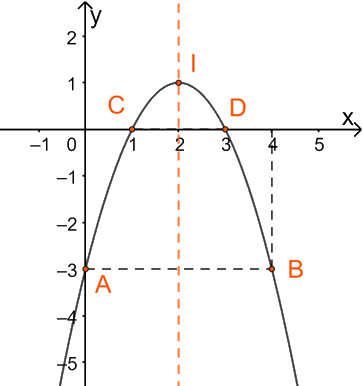
b) Hàm số \(y = - {x^2} + 4x - 3\) có \(a = - 1;b = 4;c = - 3\) và \( - \frac{b}{{2a}} = - \frac{4}{{2.( - 1)}} = 2\)
+ Đỉnh của parabol là \(I\left( {2; - {2^2} + 4.2 - 3} \right) = \left( {2;1} \right)\)
+ Trục đối xứng \(x = 2\)
+ Giao điểm với trục tung là A(0;-3)
+ Điểm đối xứng với A(0;-3) qua trục đối xứng \(x = 2\) là B(4;-3)
+ Giao điểm với trục hoành là C(1;0) và D(3;0)
Từ đó ta có đồ thị hàm số:
Bài 50 trang 62 SBT Toán 10 Cánh Diều thuộc chương trình học về vectơ trong không gian. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản về vectơ, bao gồm:
Trước khi bắt tay vào giải bài 50 trang 62 SBT Toán 10 Cánh Diều, học sinh cần đọc kỹ đề bài, xác định rõ các yếu tố đã cho và yêu cầu của bài toán. Sau đó, lựa chọn phương pháp giải phù hợp. Thông thường, các bài toán về vectơ trong không gian có thể được giải bằng các phương pháp sau:
(Nội dung lời giải chi tiết bài 50 trang 62 SBT Toán 10 Cánh Diều sẽ được trình bày tại đây. Bao gồm các bước giải, giải thích rõ ràng từng bước, và kết luận.)
Để giúp học sinh hiểu rõ hơn về cách giải bài toán vectơ trong không gian, chúng ta cùng xem xét một số ví dụ minh họa và bài tập tương tự:
Cho hai vectơ a = (1; 2; 3) và b = (-2; 1; 0). Tính tích vô hướng của hai vectơ này.
Giải:
a.b = (1)(-2) + (2)(1) + (3)(0) = -2 + 2 + 0 = 0. Vậy tích vô hướng của hai vectơ a và b bằng 0.
Cho tam giác ABC có A(1; 2; 3), B(2; 3; 4), C(3; 4; 5). Tính độ dài cạnh AB.
Khi giải bài tập về vectơ, học sinh cần lưu ý một số điều sau:
Bài 50 trang 62 SBT Toán 10 Cánh Diều là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng giải toán về vectơ trong không gian. Hy vọng với hướng dẫn chi tiết và phương pháp giải được trình bày ở trên, các em học sinh sẽ tự tin hơn khi đối mặt với bài toán này và các bài toán tương tự.
| Công thức | Mô tả |
|---|---|
| a + b = (x1 + x2; y1 + y2; z1 + z2) | Phép cộng vectơ |
| k.a = (kx1; ky1; kz1) | Phép nhân vectơ với một số thực |
| a.b = x1x2 + y1y2 + z1z2 | Tích vô hướng của hai vectơ |