Bài 17 trang 30 SBT Toán 10 Cánh Diều là một bài tập quan trọng trong chương trình học Toán 10, tập trung vào việc rèn luyện kỹ năng về vectơ và các phép toán vectơ. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các bài toán thực tế, giúp củng cố và nâng cao hiểu biết về vectơ.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 17 trang 30 SBT Toán 10 Cánh Diều, giúp các em học sinh tự tin hơn trong quá trình học tập và làm bài tập.
a) Biểu diễn miền nghiệm của hệ bất phương trình
Đề bài
a) Biểu diễn miền nghiệm của hệ bất phương trình \(\left\{ {\begin{array}{*{20}{c}}{x + y \le 5}\\{3x + 2y \le 12}\\{x \ge 1}\\{y \ge 0}\end{array}} \right.\left( {III} \right)\)
b) Tìm x, y là nghiệm của hệ bất phương trình (III) sao cho \(F = 3x + 7y\) đạt giá trị lớn nhất, nhỏ nhất.
Phương pháp giải - Xem chi tiết
a)
b)
- Biểu diễn miền nghiệm của hệ bất phương trình trên hệ tọa độ
\(F\left( {x;y} \right)\) đạt max hoặc min tại một trong các đỉnh nên ta chỉ cần tính giá trị của \(F\left( {x;y} \right)\) tại các đỉnh đó
Lời giải chi tiết
a) Ta vẽ bốn đường thẳng:
d1: x + y = 5 là đường thẳng đi qua hai điểm có tọa độ (0; 5) và (5; 0);
d2: 3x + 2y = 12 là đường thẳng đi qua hai điểm có tọa độ (4; 0) và (0; 6);
d3: x = 1 là đường thẳng song song với trục tung và đi qua điểm (1; 0);
d4: y = 0 là trục hoành.
Ta xác định từng miền nghiệm của từng bất phương trình trong hệ, gạch đi các phần không thuộc miền nghiệm của mỗi bất phương trình.
Miền nghiệm của hệ bất phương trình là miền trong tứ giác ABCD với A(1; 0), B(1; 4), C(2; 3) và D(4; 0) như hình vẽ sau:
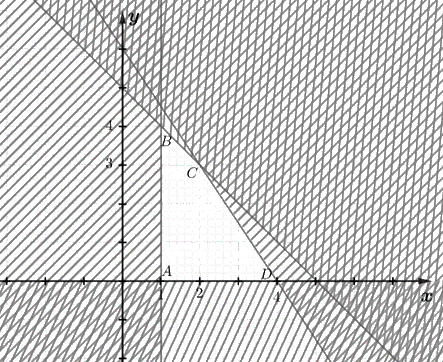
b) Ta có biểu thức F = 3x + 7y đạt giá trị lớn nhất, giá trị nhỏ nhất tại một trong các đỉnh của tứ giác ABCD.
Tại A(1; 0) với x = 1 và y = 0 thì F = 3.1 + 7.0 = 3;
Tại B(1; 4) với x = 1 và y = 4 thì F = 3.1 + 7.4 = 31;
Tại C(2; 3) với x = 2 và y = 3 thì F = 3.2 + 7.3 = 27;
Tại D(4; 0) với x = 4 và y = 0 thì F = 3.4 + 7.0 = 12.
Vậy giá trị lớn nhất của F là 31 tại x = 1 và y = 4, giá trị nhỏ nhất của F là 3 tại x = 1 và y = 0
Bài 17 trang 30 SBT Toán 10 Cánh Diều thuộc chương trình học Toán 10, tập trung vào việc ứng dụng các kiến thức về vectơ trong không gian. Bài tập này thường yêu cầu học sinh xác định các vectơ, thực hiện các phép toán cộng, trừ, nhân vectơ với một số, và tính độ dài của vectơ. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các định nghĩa, tính chất và công thức liên quan đến vectơ.
Bài tập 17 thường bao gồm các câu hỏi liên quan đến việc:
Để giải bài tập 17 trang 30 SBT Toán 10 Cánh Diều một cách hiệu quả, học sinh có thể áp dụng các phương pháp sau:
Ví dụ: Cho hai vectơ a = (1; 2) và b = (-3; 4). Tính a + b và a - b.
Giải:
a + b = (1 + (-3); 2 + 4) = (-2; 6)
a - b = (1 - (-3); 2 - 4) = (4; -2)
Việc giải bài tập về vectơ không chỉ giúp học sinh củng cố kiến thức về vectơ mà còn rèn luyện kỹ năng giải quyết vấn đề, tư duy logic và khả năng ứng dụng kiến thức vào thực tế. Đây là những kỹ năng quan trọng không chỉ trong môn Toán mà còn trong nhiều lĩnh vực khác của cuộc sống.
Giaitoan.edu.vn là một website học Toán online uy tín, cung cấp lời giải chi tiết, dễ hiểu cho các bài tập Toán 10, bao gồm cả bài 17 trang 30 SBT Toán 10 Cánh Diều. Chúng tôi cam kết mang đến cho bạn những trải nghiệm học tập tốt nhất, giúp bạn tự tin hơn trong quá trình học tập và đạt kết quả cao trong các kỳ thi.
| Công thức | Mô tả |
|---|---|
| a = (x; y) | Tọa độ của vectơ a |
| a + b = (x1 + x2; y1 + y2) | Phép cộng vectơ |
| ka = (kx; ky) | Phép nhân vectơ với một số |
| |a| = √(x2 + y2) | Độ dài của vectơ |
Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ tự tin hơn trong việc giải bài 17 trang 30 SBT Toán 10 Cánh Diều. Chúc các em học tập tốt!