Bài 23 trang 31 SBT Toán 10 Cánh Diều là một bài tập quan trọng trong chương trình học Toán 10. Bài tập này yêu cầu học sinh vận dụng kiến thức về vectơ, các phép toán vectơ và ứng dụng của vectơ trong hình học để giải quyết các bài toán cụ thể.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 23 trang 31 SBT Toán 10 Cánh Diều, giúp các em học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Phần không bị gạch (kể cả tia AB, AC) ở Hình 12 là miền nghiệm của hệ bất phương trình:
Đề bài
Phần không bị gạch (kể cả tia AB, AC) ở Hình 12 là miền nghiệm của hệ bất phương trình:
A. \(\left\{ {\begin{array}{*{20}{c}}{x + 2y \ge 2}\\{y \ge - 1}\end{array}} \right.\) B. \(\left\{ {\begin{array}{*{20}{c}}{x + 2y \le 2}\\{y \ge - 1}\end{array}} \right.\) C. \(\left\{ {\begin{array}{*{20}{c}}{2x + y < 2}\\{y > - 1}\end{array}} \right.\) D. \(\left\{ {\begin{array}{*{20}{c}}{2x + y > 2}\\{y \ge - 1}\end{array}} \right.\) | 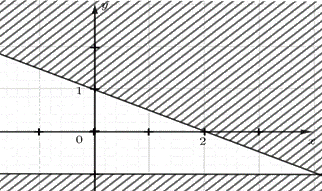 |
Hình 12 |
Phương pháp giải - Xem chi tiết
Tìm phương trình của hai đường thẳng trong hình vé
Xét điểm thuộc miền nghiệm và kết luận
Lời giải chi tiết
Gọi d là đường thẳng đi qua hai điểm A và B, vì đường thẳng này cắt hai trục tọa độ Ox, Oy lần lượt tại các điểm có tọa độ là (2; 0) và (0; 1) nên có phương trình là: \(\frac{x}{2} + \frac{y}{2} = 1 \Leftrightarrow x + 2y = 2\)
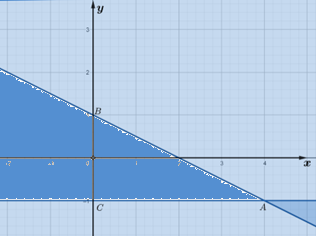
Lấy O(0; 0) có 0 + 2.0 = 0 < 2 và điểm O thuộc miền nghiệm của hệ bất phương trình và miền nghiệm kể cả đường thẳng d nên ta có bất phương trình x + 2y ≤ 2 (1).
Gọi d’ là đường thẳng đi qua hai điểm A và C và song song với trục hoành Ox nên có phương trình y = – 1.
Lấy điểm O(0; 0) có 0 > – 1 và điểm O thuộc miền nghiệm của hệ bất phương trình và miền nghiệm kể cả đường thẳng d nên ta có bất phương trình y ≥ – 1 (2).
Từ (1) và (2) ta có hệ bất phương trình: \(\left\{ {\begin{array}{*{20}{c}}{x + 2y \le 2}\\{y \ge - 1}\end{array}} \right.\)
Chọn B
Bài 23 trang 31 SBT Toán 10 Cánh Diều thuộc chương trình học về vectơ trong không gian. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản về vectơ, bao gồm:
Bài 23 thường bao gồm các dạng bài tập sau:
Để giúp học sinh hiểu rõ hơn về cách giải bài 23 trang 31 SBT Toán 10 Cánh Diều, chúng ta sẽ đi qua từng phần của bài tập với lời giải chi tiết:
Độ dài của vectơ a được tính theo công thức: |a| = √(x² + y² + z²)
Trong trường hợp này, |a| = √(2² + (-3)² + 1²) = √(4 + 9 + 1) = √14
Tích vô hướng của a và b được tính theo công thức: a.b = x₁x₂ + y₁y₂ + z₁z₂
Trong trường hợp này, a.b = (1)(-1) + (2)(0) + (3)(2) = -1 + 0 + 6 = 5
Tọa độ của vectơ AB được tính theo công thức: AB = (xB - xA; yB - yA; zB - zA)
Trong trường hợp này, AB = (4 - 1; 5 - 2; 6 - 3) = (3; 3; 3)
Để giải các bài tập về vectơ một cách hiệu quả, học sinh nên:
Khi giải bài tập về vectơ, học sinh cần lưu ý:
Bài 23 trang 31 SBT Toán 10 Cánh Diều là một bài tập quan trọng giúp học sinh củng cố kiến thức về vectơ và ứng dụng của vectơ trong hình học. Bằng cách nắm vững các khái niệm cơ bản, thành thạo các phép toán vectơ và luyện tập thường xuyên, học sinh có thể giải quyết bài tập này một cách dễ dàng và hiệu quả. Giaitoan.edu.vn hy vọng rằng với lời giải chi tiết và phương pháp giải khoa học này, các em học sinh sẽ học tập tốt môn Toán 10.