Bài 19 trang 48 SBT Toán 10 Cánh Diều là một bài tập quan trọng trong chương trình học Toán 10, tập trung vào việc vận dụng các kiến thức về vectơ để giải quyết các bài toán hình học. Bài tập này đòi hỏi học sinh phải nắm vững các khái niệm về vectơ, phép toán vectơ và ứng dụng của chúng trong việc chứng minh các tính chất hình học.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 19 trang 48 SBT Toán 10 Cánh Diều, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Trong một công trình, người ta xây dựng một cổng ra vào hình parabol (minh họa ở Hình 13) sao cho khoảng cách giữa hai chân cổng BC là 9 m
Đề bài
Trong một công trình, người ta xây dựng một cổng ra vào hình parabol (minh họa ở Hình 13) sao cho khoảng cách giữa hai chân cổng BC là 9 m. Từ một điểm M trên thân cổng người ta đo được khoảng cách tới mặt đất là MK = 1,6 m và khoảng cách từ K tới chân cổng gần nhất là BK = 0,5 m. Tính chiều cao của cổng theo đơn vị mét (làm tròn kết quả đến hàng phần mười).
Phương pháp giải - Xem chi tiết
Gắn hệ trục tọa độ cho cổng parabol, lập phương trình parabol thể hiện cổng.
Lời giải chi tiết
Đặt hệ trục tọa độ như hình vẽ:
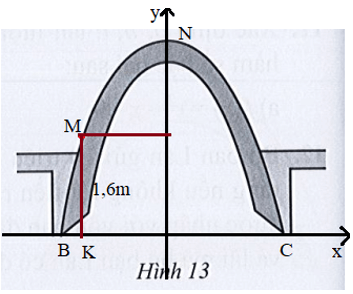
Tọa độ các điểm lần lượt là: B(– 4,5; 0); C(4,5; 0);
Vì BK = 0,5 m nên OK = 4,5 – 0,5 = 4 m. Do đó M(4; 1,6).
Cổng có hình parabol nên gọi phương trình hàm số là \(y = a{x^2} + bx + c\) (a ≠ 0) (1).
Điểm B thuộc parabol nên thay tọa độ điểm B vào (1) ta được:
\(a{( - 4,5)^2} + b( - 4,5) + c = 0 \Leftrightarrow 20,25a - 4,5b + c = 0\) (2).
Điểm C thuộc parabol nên thay tọa độ điểm C vào (1) ta được:
\(a{( 4,5)^2} + b( 4,5) + c = 0 \Leftrightarrow 20,25a + 4,5b + c = 0\) (3).
Điểm M thuộc parabol nên thay tọa độ điểm M vào (1) ta được:
\(1,6 = a{.4^2} + b.4 + c \Leftrightarrow 16a + 4b + c = 0\) (4).
Từ (2), (3) và (4) ta có hệ:
\(\left\{ {\begin{array}{*{20}{c}}{20,25 - 4,5b + c = 0}\\{20,25 + 4,5b + c = 0}\\{16a + 4b + c = 1,6}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a = - \frac{{32}}{{85}}}\\{b = 0}\\{c = \frac{{648}}{{85}}}\end{array}} \right.} \right.\)
Suy ra parabol cần tìm là \(y = \frac{{ - 32}}{{85}}{x^2} + \frac{{648}}{{85}}\).
Điểm N là điểm đỉnh của parabol thuộc vào trục tung Oy nên hoành độ điểm N bằng 0.
Thay x = 0 vào hàm số ta được \(y = \frac{{648}}{{85}}\), đó cũng chính là chiều cao của cổng.
Vậy chiều cao của cổng khoảng 7,6 m.
Bài 19 trang 48 SBT Toán 10 Cánh Diều thuộc chương trình học Toán 10, tập trung vào việc ứng dụng kiến thức về vectơ trong hình học. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản về vectơ, bao gồm:
Bài 19 trang 48 SBT Toán 10 Cánh Diều thường bao gồm các dạng bài tập sau:
Để giúp các em học sinh hiểu rõ hơn về cách giải bài tập này, chúng ta sẽ đi vào giải chi tiết từng phần của bài 19 trang 48 SBT Toán 10 Cánh Diều. (Nội dung giải chi tiết sẽ được trình bày ở đây, bao gồm từng bước giải, giải thích rõ ràng và các lưu ý quan trọng. Ví dụ:)
Đề bài: Cho tam giác ABC. Chứng minh rằng: overrightarrow{AB} +overrightarrow{BC} =overrightarrow{AC}
Lời giải:
Áp dụng quy tắc cộng vectơ, ta có:
overrightarrow{AB} +overrightarrow{BC} là vectơ tổng có điểm đầu là A và điểm cuối là C. Do đó:
overrightarrow{AB} +overrightarrow{BC} =overrightarrow{AC} (điều phải chứng minh)
Để giải các bài tập về vectơ một cách hiệu quả, các em học sinh nên:
Ngoài sách giáo khoa và sách bài tập, các em học sinh có thể tham khảo thêm các tài liệu sau để học tốt môn Toán 10:
Bài 19 trang 48 SBT Toán 10 Cánh Diều là một bài tập quan trọng giúp các em học sinh củng cố kiến thức về vectơ và rèn luyện kỹ năng giải toán. Hy vọng với lời giải chi tiết và phương pháp giải hiệu quả mà Giaitoan.edu.vn cung cấp, các em sẽ tự tin hơn trong việc học tập và đạt kết quả tốt trong môn Toán 10.