Bài 2 trang 42 SBT Toán 10 Cánh Diều là một bài tập quan trọng trong chương trình học Toán 10, tập trung vào việc rèn luyện kỹ năng về tập hợp và các phép toán trên tập hợp. Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập này, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Chúng tôi cung cấp không chỉ đáp án mà còn cả phương pháp giải, giúp các em hiểu rõ bản chất của bài toán và áp dụng vào thực tế.
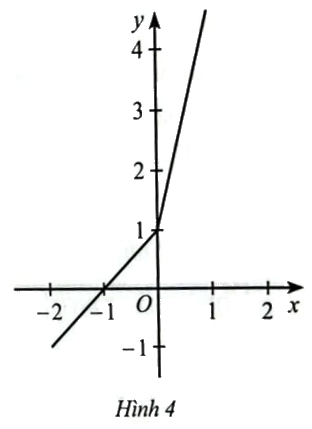
Cho đồ thị hàm số \(y = f\left( x \right)\) ở Hình 4. Phát biểu nào sau đây là đúng?
Đề bài
Cho đồ thị hàm số \(y = f\left( x \right)\) ở Hình 4. Phát biểu nào sau đây là đúng?
A. Đồ thị hàm số cắt trục hoành tại điểm của hoành độ bằng 1
B. Đồ thị hàm số cắt trục tung tại điểm có tung bộ bằng -1
C. Hàm số đồng biến trên khoảng \(\left( { - 1; + \infty } \right)\), ngịch biến trên khoảng \(\left( { - \infty ; - 1} \right)\)
D. Hàm số đồng biến trên \(\mathbb{R}\)
Phương pháp giải - Xem chi tiết
Hàm số \(f\left( x \right)\) đồng biến trên \(\left( {a;b} \right)\) khi \(\forall {x_1},{x_2} \in \left( {a;b} \right),{x_1} < {x_2} \Rightarrow f\left( {{x_1}} \right) < f\left( {{x_2}} \right)\)
Hàm số \(f\left( x \right)\) nghịch biến trên \(\left( {a;b} \right)\) khi \(\forall {x_1},{x_2} \in \left( {a;b} \right),{x_1} < {x_2} \Rightarrow f\left( {{x_1}} \right) > f\left( {{x_2}} \right)\)
Lời giải chi tiết
Đồ thị hàm số cắt trục hoành tại điểm có tọa độ (-1;0) => A sai
Đồ thị hàm số cắt trục tung tại điểm có tọa độ (0;1) => B sai
Quan sát đồ thị, ta thấy: Đồ thị hàm số đi lên từ trái sang phải => Hàm số đồng biến trên \(\mathbb{R}\)
Chọn D.
Bài 2 trang 42 SBT Toán 10 Cánh Diều yêu cầu học sinh xác định các tập hợp và thực hiện các phép toán hợp, giao, hiệu của các tập hợp. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững định nghĩa và tính chất của các phép toán này.
Cho các tập hợp A = {1; 2; 3; 4; 5}, B = {2; 4; 6; 8} và C = {1; 3; 5; 7; 9}. Hãy tìm:
Để giải các bài tập về tập hợp, chúng ta cần:
a) A ∪ B (Hợp của A và B) là tập hợp chứa tất cả các phần tử thuộc A hoặc B (hoặc cả hai).
A ∪ B = {1; 2; 3; 4; 5; 6; 8}
b) A ∩ B (Giao của A và B) là tập hợp chứa tất cả các phần tử thuộc cả A và B.
A ∩ B = {2; 4}
c) A \ B (Hiệu của A và B) là tập hợp chứa tất cả các phần tử thuộc A nhưng không thuộc B.
A \ B = {1; 3; 5}
d) B \ A (Hiệu của B và A) là tập hợp chứa tất cả các phần tử thuộc B nhưng không thuộc A.
B \ A = {6; 8}
Giả sử ta có hai tập hợp:
Thì:
Ngoài các phép toán cơ bản như hợp, giao, hiệu, còn có các phép toán khác như phần bù, tích Descartes. Việc hiểu rõ các phép toán này sẽ giúp các em giải quyết các bài tập phức tạp hơn về tập hợp.
Để củng cố kiến thức về tập hợp, các em nên luyện tập thêm các bài tập khác trong sách bài tập và các nguồn tài liệu học tập khác. Việc luyện tập thường xuyên sẽ giúp các em nắm vững kiến thức và tự tin giải các bài tập tương tự.
Hy vọng với hướng dẫn chi tiết này, các em học sinh sẽ hiểu rõ cách giải bài 2 trang 42 SBT Toán 10 - Cánh Diều và tự tin hơn trong việc học tập môn Toán.