Bài 26 trang 85 SBT Toán 10 Cánh Diều là một bài tập quan trọng trong chương trình học Toán 10. Bài tập này yêu cầu học sinh vận dụng kiến thức về vectơ, các phép toán vectơ và ứng dụng của vectơ trong hình học để giải quyết các bài toán cụ thể.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 26 trang 85 SBT Toán 10 Cánh Diều, giúp các em học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Cho điểm I là trung điểm của đoạn thẳng AB. Phát biểu nào sau đây là đúng?
Đề bài
Cho điểm I là trung điểm của đoạn thẳng AB. Phát biểu nào sau đây là đúng?
A. \(\overrightarrow {IA} = \overrightarrow {IB} \)
B. \(\overrightarrow {IA} \) và \(\overrightarrow {IB} \) cùng hướng
C. \(\overrightarrow {AI} = \overrightarrow {BI} \)
D. \(\overrightarrow {AI} = \overrightarrow {IB} \)
Phương pháp giải - Xem chi tiết
Dựa vào định nghĩa hai vectơ bằng nhau để tìm câu đúng
Lời giải chi tiết
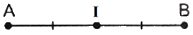
Nếu I là trung điểm của đoạn thẳng AB thì \(\overrightarrow {AI} = \overrightarrow {IB} \)
Chọn D
Bài 26 trang 85 SBT Toán 10 Cánh Diều thuộc chương trình học về vectơ trong không gian. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản về vectơ, bao gồm:
Bài 26 thường yêu cầu học sinh áp dụng các kiến thức này để giải các bài toán liên quan đến tìm tọa độ điểm, chứng minh các đẳng thức vectơ, hoặc tính góc giữa các vectơ.
Để cung cấp lời giải chi tiết, chúng ta cần xem xét nội dung cụ thể của bài toán. Tuy nhiên, dựa trên cấu trúc chung của SBT Toán 10 Cánh Diều, bài 26 thường bao gồm các dạng bài sau:
Ví dụ: Cho A(1; 2; 3) và B(4; 5; 6). Tìm tọa độ điểm M sao cho M là trung điểm của đoạn AB.
Lời giải:
Áp dụng công thức trung điểm, ta có:
M = ((xA + xB)/2; (yA + yB)/2; (zA + zB)/2) = ((1+4)/2; (2+5)/2; (3+6)/2) = (2.5; 3.5; 4.5)
Ví dụ: Chứng minh rằng với mọi điểm O, ta có: OA + OB = 2OM, với M là trung điểm của AB.
Lời giải:
Vì M là trung điểm của AB, ta có: AM = MB. Do đó, AM = (1/2)AB. Suy ra AB = 2AM. Ta có: OA + OB = OA + (OA + AB) = 2OA + AB = 2OA + 2AM = 2(OA + AM) = 2OM.
Ví dụ: Cho hai vectơ a = (1; 2; 3) và b = (4; 5; 6). Tính góc θ giữa hai vectơ a và b.
Lời giải:
Sử dụng công thức tính tích vô hướng:
a.b = |a||b|cosθ
Tính a.b = (1*4) + (2*5) + (3*6) = 4 + 10 + 18 = 32
Tính |a| = √(1² + 2² + 3²) = √14
Tính |b| = √(4² + 5² + 6²) = √77
Suy ra cosθ = 32 / (√14 * √77) ≈ 0.975
Vậy θ ≈ 12.89°
Ngoài sách giáo khoa và SBT Toán 10 Cánh Diều, học sinh có thể tham khảo thêm các tài liệu sau:
Hy vọng với lời giải chi tiết và các mẹo giải bài tập trên, các em học sinh sẽ tự tin hơn khi giải bài 26 trang 85 SBT Toán 10 Cánh Diều và đạt kết quả tốt trong môn Toán.