Bài 42 trang 60 SBT Toán 10 Cánh Diều là một bài tập quan trọng trong chương trình học Toán 10. Bài tập này yêu cầu học sinh vận dụng kiến thức về vectơ, các phép toán vectơ và ứng dụng của vectơ trong hình học để giải quyết các bài toán cụ thể.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 42 trang 60 SBT Toán 10 Cánh Diều, giúp các em học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Để lao lên một bức tường, bác Dũng dùng một chiếc thang cao hơn bức tường đó 2m.
Đề bài
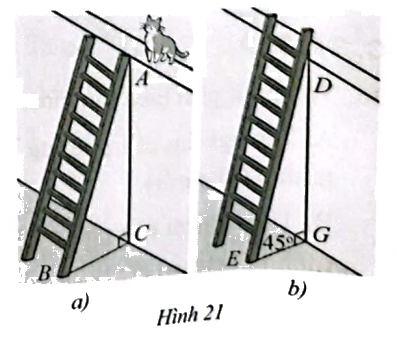
Để lao lên một bức tường, bác Dũng dùng một chiếc thang cao hơn bức tường đó 2m. Ban đầu bác Dũng đạt chiếc thang mà đầu trên của chiếc thang đó vừa chạm đúng vào mép trên của bức tường (Hình 21a). Sau đó bác Dũng dịch chuyển chân thang vào gần chân bức tường thêm 1 m thì bác Dũng thấy thang tạo với mặt đất một góc \({45^ \circ }\). Bức tường cao bao nhiêu mét?
Phương pháp giải - Xem chi tiết
Lập hàm số biểu diễn chiều khoảng cách từ chân thang đến chân thường bằng chiều cao bức tường
Giải phương trình tìm chiều cao của bức tường
Lời giải chi tiết
Gọi chiều cao bức tường là \(x\) (m) (\(x > 0\)).
Suy ra chiều dài của thang là \(x + 2\) (m)
Ta có: \(AC = x,AB = x + 2\)
Khi đặt chiếc thang mà đầu trên của chiếc thang đó chạm đúng vào mép trên của bức tường thì khoảng cách chân thang đến chân tường là: \(BC = \sqrt {A{B^2} - A{C^2}} = \sqrt {{{\left( {x + 2} \right)}^2} - {x^2}} \) (m)
Khi dịch chuyển chân thang vào gần chân bức tường thêm 1m thì
\(EG = \sqrt {{{\left( {x + 2} \right)}^2} - {x^2}} - 1\)
Khi ấy thang tạo với mặt đất góc \({45^ \circ }\) nên khoảng cách từ chân thang đến chân tường bằng chiều cao bức tường hay \(EG = x\)
Ta có phương trình \(\sqrt {{{\left( {x + 2} \right)}^2} - {x^2}} - 1 = x \Leftrightarrow \sqrt {{{\left( {x + 2} \right)}^2} - {x^2}} = x + 1\)
\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}x + 1 \ge 0\\{\left( {x + 2} \right)^2} - {x^2} = {\left( {x + 1} \right)^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge - 1\\4x + 4 = {x^2} + 2x + 1\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge - 1\\{x^2} - 2x - 3 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge - 1\\\left[ \begin{array}{l}x = - 1\;(L)\\x = 3\;\end{array} \right.\quad \end{array} \right. \Leftrightarrow x = 3\;\end{array}\)
Vậy, chiều cao của bức tường là 3 m.
Bài 42 trang 60 SBT Toán 10 Cánh Diều thuộc chương trình học về vectơ trong không gian. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản về:
Bài 42 thường bao gồm các dạng bài tập sau:
Để giúp các em học sinh hiểu rõ hơn về cách giải bài 42 trang 60 SBT Toán 10 Cánh Diều, chúng ta sẽ đi vào giải chi tiết từng phần của bài tập. (Lưu ý: Nội dung giải chi tiết sẽ được trình bày cụ thể cho từng câu hỏi trong bài tập 42, giả sử bài tập có nhiều câu hỏi. Ví dụ dưới đây chỉ mang tính minh họa.)
Câu a: Cho A(1; 2), B(3; 4). Tìm tọa độ của vectơ AB.
Giải:
Vectơ AB có tọa độ là: AB = (3 - 1; 4 - 2) = (2; 2).
Ngoài bài 42, các em học sinh có thể gặp các bài tập tương tự về vectơ trong SBT Toán 10 Cánh Diều. Để giải quyết các bài tập này, các em cần:
Để học tốt môn Toán 10, đặc biệt là phần vectơ, các em học sinh nên:
Bài 42 trang 60 SBT Toán 10 Cánh Diều là một bài tập quan trọng giúp các em học sinh củng cố kiến thức về vectơ. Hy vọng với lời giải chi tiết và các phương pháp giải được trình bày ở trên, các em sẽ tự tin hơn khi giải quyết các bài toán tương tự. Chúc các em học tập tốt!
| Công thức vectơ quan trọng | Mô tả |
|---|---|
| AB = B - A | Vectơ AB bằng hiệu tọa độ của điểm B và điểm A |
| k * AB = (kx; ky) | Nhân vectơ AB với một số thực k |