Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 10. Bài viết này sẽ hướng dẫn bạn cách giải bài 21 trang 52 trong sách bài tập (SBT) Toán 10 - Cánh Diều. Chúng tôi cam kết cung cấp nội dung chính xác và hữu ích để giúp bạn học Toán hiệu quả.
Cho hàm số \(y = f\left( x \right)\) có đồ thị ở Hình 15.
Đề bài
Cho hàm số \(y = f\left( x \right)\) có đồ thị ở Hình 15.
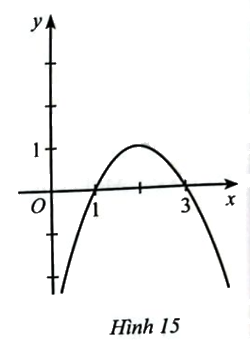
Trong các phát biểu sau, phát biểu nào là sai?
A. \(f\left( x \right) < 0\) khi và chỉ khi \(x \in \left( {1;3} \right)\)
B. \(f\left( x \right) \le 0\) khi và chỉ khi \(x \in \left( { - \infty ;1} \right] \cup \left[ {3; + \infty } \right)\)
C. \(f\left( x \right) > 0\) khi và chỉ khi \(x \in \left( {1;3} \right)\)
D. \(f\left( x \right) \ge 0\) khi và chỉ khi \(x \in \left[ {1;3} \right]\)
Phương pháp giải - Xem chi tiết
Đồ thị hàm số \(f\left( x \right) < 0\) là phần đồ thị nằm dưới trục hoành và ngược lại
Lời giải chi tiết
Hình đồ thị hàm số, ta thấy
\(f\left( x \right) < 0\) khi \(x \in \left( { - \infty ;1} \right) \cup \left( {3; + \infty } \right)\)
\(f\left( x \right) = 0\) khi \(x = 1\) hoặc \(x = 3\)
\(f\left( x \right) > 0\) khi \(x \in (1;3)\)
Chọn A.
Bài 21 trang 52 SBT Toán 10 - Cánh Diều thuộc chương trình học Toán 10, tập trung vào việc vận dụng các kiến thức về vectơ trong không gian để giải quyết các bài toán hình học. Bài tập này thường yêu cầu học sinh phải hiểu rõ các khái niệm như vectơ, phép cộng, phép trừ vectơ, tích của một số với vectơ, và các tính chất liên quan.
Bài 21 trang 52 SBT Toán 10 - Cánh Diều thường bao gồm các dạng bài tập sau:
Để giúp bạn hiểu rõ hơn về cách giải bài tập này, chúng tôi sẽ cung cấp lời giải chi tiết cho từng phần của bài 21 trang 52 SBT Toán 10 - Cánh Diều. (Lưu ý: Nội dung lời giải chi tiết sẽ được trình bày cụ thể cho từng câu hỏi trong bài tập. Do giới hạn độ dài, chúng tôi sẽ cung cấp một ví dụ minh họa.)
Đề bài: Cho hình bình hành ABCD. Gọi M là trung điểm của cạnh BC. Hãy biểu diễn vectơ AM theo hai vectơ AB và AD.
Lời giải:
Để giải tốt các bài tập về vectơ, bạn nên lưu ý những điều sau:
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập về vectơ, bạn có thể tham khảo các bài tập tương tự sau:
Hy vọng rằng bài viết này đã cung cấp cho bạn những kiến thức và kỹ năng cần thiết để giải bài 21 trang 52 SBT Toán 10 - Cánh Diều một cách hiệu quả. Chúc bạn học tập tốt và đạt kết quả cao trong môn Toán!