Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 10. Bài viết này sẽ hướng dẫn bạn giải bài 77 trang 107 SBT Toán 10 - Cánh Diều một cách nhanh chóng và hiệu quả.
Chúng tôi luôn cố gắng cung cấp nội dung chất lượng cao, giúp bạn học Toán 10 một cách tốt nhất.
Một người quan sát đứng ở bờ sông muốn đo độ rộng của khúc sông chỗ chảy qua vị trí đang đứng (khúc sông tương đối thẳng, có thể xem hai bờ song song
Đề bài
Một người quan sát đứng ở bờ sông muốn đo độ rộng của khúc sông chỗ chảy qua vị trí đang đứng (khúc sông tương đối thẳng, có thể xem hai bờ song song với nhau).
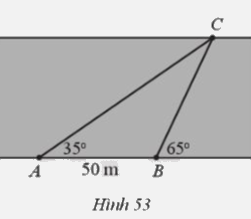
Từ vị trí đang đứng A, người đó đo được góc nghiêng \(\alpha \) = 35° so với bờ sông tới một vị trí C quan sát được ở phía bờ bên kia. Sau đó di chuyển dọc bờ sông đến vị trí B cách A một khoảng d = 50 m và tiếp tục đo được góc nghiêng \(\beta \)=65° so với bờ sông tới vị trí C đã chọn (Hình 53). Hỏi độ rộng của con sông chỗ chảy qua vị trí người quan sát đang đứng là bao nhiêu mét (làm tròn kết quả đến hàng phần trăm)?
Phương pháp giải - Xem chi tiết
Độ rộng khúc sông là chiều cao kẻ từ đỉnh C của ∆ABC
Bước 1: Tính góc \(\widehat {ABC},\widehat {ACB}\)
Bước 2: Sử dụng định lí sin để tính độ dài BC của ∆ABC
Bước 3: Tính diện tích tam giác ABC theo công thức \(S = \frac{1}{2}BC.AB.\sin \widehat {ABC}\)
Bước 4: Tính chiều cao hCcủa tam giác ABC theo công thức \(S = \frac{1}{2}AB.{h_C}\) rồi kết luận
Lời giải chi tiết
Ta có: \(\widehat {ABC} = {180^0} - {65^0} = {115^0} \Rightarrow \widehat {ACB} = {180^0} - \left( {\widehat {CAB} + \widehat {ABC}} \right) = {30^0}\)
Áp dụng định lí sin cho ∆ABC ta có: \(\frac{{BC}}{{\sin A}} = \frac{{AB}}{{\sin C}} \Rightarrow BC = \frac{{AB.\sin A}}{{\sin C}} = \frac{{50.\sin {{35}^0}}}{{\sin {{30}^0}}} \approx 57,36\) (m)
Diện tích tam giác ABC là: \(S = \frac{1}{2}BC.AB.\sin \widehat {ABC} = \frac{1}{2}.57,36.50.\sin {115^0} \approx 1299,65\) (m2)
Gọi hc là chiều cao kẻ từ đỉnh C của ∆ABC
Ta có: \(S = \frac{1}{2}AB.{h_C} \Rightarrow {h_C} = \frac{{2S}}{{AB}} \approx 51,99\) (m)
Vậy chiều rộng khúc sông là 51,99 m
Bài 77 trang 107 SBT Toán 10 - Cánh Diều thuộc chương trình học Toán 10, tập trung vào việc vận dụng các kiến thức về vectơ để giải quyết các bài toán hình học. Bài tập này yêu cầu học sinh phải nắm vững các khái niệm như vectơ, phép cộng, phép trừ vectơ, tích của một số với vectơ, và các tính chất liên quan.
Bài tập 77 thường bao gồm các dạng bài sau:
Để giải bài 77 trang 107 SBT Toán 10 - Cánh Diều, bạn cần thực hiện các bước sau:
Ví dụ minh họa:
Cho A(1; 2), B(3; 4). Tìm tọa độ của điểm C sao cho AC = 2AB.
Lời giải:
Ta có: AB = (3 - 1; 4 - 2) = (2; 2).
AC = 2AB = 2(2; 2) = (4; 4).
Gọi C(x; y). Khi đó, AC = (x - 1; y - 2).
Ta có hệ phương trình:
Giải hệ phương trình, ta được x = 5, y = 6.
Vậy C(5; 6).
Ngoài bài 77, SBT Toán 10 - Cánh Diều còn có nhiều bài tập tương tự về vectơ. Để giải các bài tập này, bạn cần nắm vững các kiến thức sau:
Khi giải bài tập về vectơ, bạn cần lưu ý những điều sau:
Bài 77 trang 107 SBT Toán 10 - Cánh Diều là một bài tập quan trọng giúp bạn củng cố kiến thức về vectơ. Hy vọng với hướng dẫn chi tiết này, bạn sẽ giải bài tập này một cách dễ dàng và hiệu quả. Chúc bạn học tốt!