Bài 8 trang 25 SBT Toán 10 Cánh Diều là một bài tập quan trọng trong chương trình học Toán 10, tập trung vào việc rèn luyện kỹ năng về vectơ và các phép toán vectơ. Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu, giúp học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Chúng tôi cung cấp không chỉ đáp án mà còn cả phương pháp giải, giúp bạn hiểu rõ bản chất của bài toán và áp dụng vào các tình huống khác nhau.
Nửa mặt phẳng không bị gạch (không kể d) ở mỗi Hình 5a, 5b, 5c là miền nghiệm của bất phương trình nào?
Đề bài
Nửa mặt phẳng không bị gạch (không kể d) ở mỗi Hình 5a, 5b, 5c là miền nghiệm của bất phương trình nào?
 |  |  |
a) | b) | c) |
Phương pháp giải - Xem chi tiết
Lời giải chi tiết
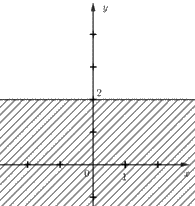
+ Hình 8a): Đường thẳng d song song với trục Ox và đi qua điểm (0; 2) nên d là y = 2 hay 0.x + 1.y = 2.
Lấy O(0; 0) có 0.0 + 1.0 = 0 < 2.
Quan sát trên Hình 8a) ta thấy điểm O(0; 0) không thuộc miền nghiệm của bất phương trình và không kể đường thẳng d nên bất phương trình cần tìm là: y > 2.
Vậy bất phương trình có miền nghiệm được biểu diễn ở Hình 8a) là y > 2.
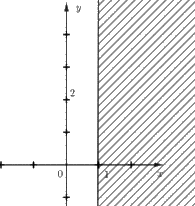
+ Hình 8b): Đường thẳng d song song với trục Oy và đi qua điểm (1; 0) nên d là x = 1 hay x + 0.y = 1.
Lấy O(0; 0) có 1.0 + 0.0 = 0 < 1.
Quan sát trên Hình 8b) ta thấy điểm O(0; 0) thuộc miền nghiệm của bất phương trình và không kể đường thẳng d nên bất phương trình cần tìm là: x < 1.
Vậy bất phương trình có miền nghiệm được biểu diễn ở Hình 8b) là x < 1.
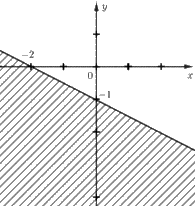
+) Hình 8c): Gọi phương trình đường thẳng d có dạng: \(y = ax + b\left( {a \ne 0} \right)\)
Đường thẳng d là đường thẳng đi qua hai điểm có tọa độ (– 2; 0) nên thay tọa độ điểm này vào phương trình d ta được: \(0 = a.\left( { - 2} \right) + b \Leftrightarrow - 2a + b = 0\left( 1 \right)\)
Đường thẳng d là đường thẳng đi qua hai điểm có tọa độ (0; – 1) nên thay tọa độ điểm này vào phương trình d ta được: \( - 1 = a.0 + b \Leftrightarrow b = - 1\)
Thay b = 0 – 1 vào (1) ta được \( - 2a + \left( { - 1} \right) = 0 \Leftrightarrow a = - \frac{1}{2}\).
Suy ra phương trình đường thẳng d là \(y = - \frac{1}{2}x - 1\) hay \(\frac{1}{2}x + y = - 1\)
Lấy O(0; 0) có \(\frac{1}{2}.0 + 0 = 0 > - 1\)
Quan sát trên Hình 8c) ta thấy điểm O(0; 0) thuộc nửa mặt phẳng là miền nghiệm của bất phương trình và không kể đường thẳng d nên bất phương trình cần tìm là: \(\frac{1}{2}x + y > - 1\)
Vậy bất phương trình có miền nghiệm được biểu diễn ở Hình 8c) là \(\frac{1}{2}x + y > - 1\)
Bài 8 trang 25 SBT Toán 10 Cánh Diều thuộc chương trình học về vectơ trong không gian. Bài tập này yêu cầu học sinh vận dụng kiến thức về các phép toán vectơ như cộng, trừ, nhân với một số thực, và tính độ dài của vectơ để giải quyết các bài toán cụ thể. Việc nắm vững các khái niệm và công thức liên quan đến vectơ là điều kiện cần thiết để hoàn thành tốt bài tập này.
Bài 8 trang 25 SBT Toán 10 Cánh Diều thường bao gồm các dạng bài tập sau:
Để giúp học sinh hiểu rõ hơn về cách giải bài 8 trang 25 SBT Toán 10 Cánh Diều, chúng ta sẽ đi qua từng phần của bài tập với lời giải chi tiết:
Đề bài: Cho hai vectơ a = (1; 2) và b = (-3; 4). Tính a + b.
Lời giải:
a + b = (1 + (-3); 2 + 4) = (-2; 6)
Đề bài: Cho vectơ a = (2; -1) và số thực k = 3. Tính ka.
Lời giải:
ka = 3(2; -1) = (3*2; 3*(-1)) = (6; -3)
Đề bài: Tính độ dài của vectơ a = (3; -4).
Lời giải:
|a| = √((3)^2 + (-4)^2) = √(9 + 16) = √25 = 5
Để giải tốt các bài tập về vectơ, bạn cần nắm vững các kiến thức sau:
Để củng cố kiến thức, bạn có thể tự giải các bài tập tương tự sau:
Bài 8 trang 25 SBT Toán 10 Cánh Diều là một bài tập cơ bản nhưng quan trọng trong chương trình học Toán 10. Việc nắm vững kiến thức và kỹ năng giải bài tập về vectơ sẽ giúp bạn tự tin hơn trong việc học tập và giải quyết các vấn đề liên quan đến vectơ trong các lĩnh vực khác nhau.