Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 10. Bài viết này sẽ hướng dẫn bạn cách giải bài 27 trang 52 trong sách bài tập (SBT) Toán 10 - Cánh Diều. Chúng tôi cam kết cung cấp nội dung chính xác và hữu ích để giúp bạn học Toán hiệu quả.
Bộ phận nghiên cứu thị trường của một xí nghiệp xác định tổng chi phí để sản xuất \(Q\) sản phẩm là \({Q^2} + 200Q + 180.000\) (nghìn đồng).
Đề bài
Bộ phận nghiên cứu thị trường của một xí nghiệp xác định tổng chi phí để sản xuất \(Q\) sản phẩm là \({Q^2} + 200Q + 180.000\) (nghìn đồng). Giả sử giá mỗi sản phẩm bán ra thị trường là 1 300 nghìn đồng
a) Xác định lợi nhuận xí nghiệp thu được sau khi bán hết \(Q\) sản phẩm đó, biết rằng lợi nhuận là hiệu doanh thu trừ đi tổng chi phí để sản xuất
b) Xí nghiệp cần sản xuất bao nhiêu sản phẩm để không bị lỗ? Biết rằng các sản phẩm được sản xuất ra đều bán hết
Phương pháp giải - Xem chi tiết
Xác định hàm doanh thu, từ đó xác định lợi nhuận DN thu được
Doanh nghiêp không bị lỗ khi Lợi nhuận không âm, từ đó giải hệ bất phương trình
Lời giải chi tiết
a) Doanh thu của xí nghiệp là: \(DT = 1\;300Q\) (nghìn đồng)
Tổng chi phí để sản xuất \(Q\) sản phẩm là \(CP = {Q^2} + 200Q + 180\;000\) (nghìn đồng)
\( \Rightarrow \) Lợi nhuận của xí nghiệp là: \(f\left( Q \right) = DT - CP = 1300Q - \left( {{Q^2} + 200Q + 180000} \right) = - {Q^2} + 1100Q - 180000\) (nghìn đồng)
b) Xí nghiệp không bị lỗ khi và chỉ khi \(f\left( Q \right) \ge 0\)
\(f\left( x \right) = - {x^2} + 1\;100x - 180\;000\)có hai nghiệm \({x_1} = 200;{x_2} = 900\) và có hệ số \(a = - 1 < 0\)
Ta có bảng xét dấu của \(f\left( x \right)\) như sau:
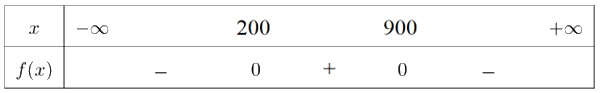
Theo đó, \(f\left( Q \right) \ge 0 \Leftrightarrow Q \in \left[ {200;900} \right]\).
Vậy ví nghiệp cần sản xuất số sản phẩm trong đoạn \(\left[ {200;900} \right]\) để không bị lỗ
Bài 27 trang 52 SBT Toán 10 - Cánh Diều thuộc chương trình học Toán 10, tập trung vào việc vận dụng các kiến thức về vectơ trong mặt phẳng để giải quyết các bài toán hình học. Bài tập này thường yêu cầu học sinh hiểu rõ các khái niệm như vectơ, phép cộng, phép trừ vectơ, tích của một số với vectơ, và các tính chất liên quan.
Bài 27 thường bao gồm các dạng bài tập sau:
Để giúp bạn hiểu rõ hơn, chúng ta sẽ đi vào giải chi tiết từng phần của bài 27. (Lưu ý: Vì bài tập cụ thể không được cung cấp, phần này sẽ trình bày cách tiếp cận chung và các bước giải quyết các dạng bài tập thường gặp.)
Đề bài: Cho tam giác ABC. Xác định các vectơ \overrightarrow{AB}", "\overrightarrow{BC}", "\overrightarrow{CA}".
Lời giải:
Vectơ \overrightarrow{AB}" là vectơ có điểm gốc là A và điểm cuối là B. Tương tự, vectơ \overrightarrow{BC}" có điểm gốc là B và điểm cuối là C, vectơ \overrightarrow{CA}" có điểm gốc là C và điểm cuối là A.
Đề bài: Cho \overrightarrow{a} = (1; 2)" và \overrightarrow{b} = (-3; 1)". Tính \overrightarrow{a} + \overrightarrow{b}" và 2\overrightarrow{a}".
Lời giải:
\overrightarrow{a} + \overrightarrow{b} = (1 + (-3); 2 + 1) = (-2; 3)"
2\overrightarrow{a} = (2*1; 2*2) = (2; 4)"
Đề bài: Chứng minh rằng \overrightarrow{AB} + \overrightarrow{BC} = \overrightarrow{AC}".
Lời giải:
Theo quy tắc cộng vectơ, nếu B nằm giữa A và C thì \overrightarrow{AB} + \overrightarrow{BC} = \overrightarrow{AC}". Điều này có nghĩa là vectơ tổng của \overrightarrow{AB}" và \overrightarrow{BC}" là vectơ nối từ A đến C.
Đề bài: Chứng minh rằng ba điểm A, B, C thẳng hàng.
Lời giải:
Để chứng minh A, B, C thẳng hàng, ta cần chứng minh rằng có một vectơ cùng phương với một vectơ khác và có cùng điểm gốc. Ví dụ, ta có thể chứng minh \overrightarrow{AB}" và \overrightarrow{AC}" cùng phương.
Hy vọng với hướng dẫn chi tiết này, bạn đã có thể tự tin giải bài 27 trang 52 SBT Toán 10 - Cánh Diều. Hãy luyện tập thường xuyên để củng cố kiến thức và đạt kết quả tốt nhất trong môn Toán.