Bài 54 trang 100 SBT Toán 10 Cánh Diều là một bài tập quan trọng trong chương trình học Toán 10. Bài tập này yêu cầu học sinh vận dụng kiến thức về vectơ, các phép toán vectơ và ứng dụng của vectơ trong hình học để giải quyết các bài toán cụ thể.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 54 trang 100 SBT Toán 10 Cánh Diều, giúp các em học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Cho hình bình hành ABCD. Lấy các điểm M, N, P thoả mãn \(\overrightarrow {AM} = \frac{1}{2}\overrightarrow {AB} ,\overrightarrow {AN} = \frac{1}{5}\overrightarrow {AC} ,\overrightarrow {AP} = \frac{1}{3}\overrightarrow {AD} \). Đặt \(\overrightarrow {AB} = \overrightarrow a ,\overrightarrow {AD} = \overrightarrow b \). Biểu thị các vectơ \(\overrightarrow {AN} ,\overrightarrow {MN} ,\overrightarrow {NP} \) theo các vectơ \(\overrightarrow a ,\overrightarrow b \) và chứng minh ba điểm M, N,
Đề bài
Cho hình bình hành ABCD. Lấy các điểm M, N, P thoả mãn \(\overrightarrow {AM} = \frac{1}{2}\overrightarrow {AB} ,\overrightarrow {AN} = \frac{1}{5}\overrightarrow {AC} ,\overrightarrow {AP} = \frac{1}{3}\overrightarrow {AD} \). Đặt \(\overrightarrow {AB} = \overrightarrow a ,\overrightarrow {AD} = \overrightarrow b \). Biểu thị các vectơ \(\overrightarrow {AN} ,\overrightarrow {MN} ,\overrightarrow {NP} \) theo các vectơ \(\overrightarrow a ,\overrightarrow b \) và chứng minh ba điểm M, N, P thẳng hàng.
Phương pháp giải - Xem chi tiết
Bước 1: Xác định vị trí các điểm M, N, P trên các cạnh AB, AC, AD
Bước 2: Sử dụng các quy tắc để biểu diễn các vectơ theo \(\overrightarrow {AB} \) và \(\overrightarrow {AD} \)
Bước 3: Sử dụng điều kiện \(\overrightarrow {MN} = k\overrightarrow {NP} \) chứng minh M, N, P thẳng hàng.
Lời giải chi tiết
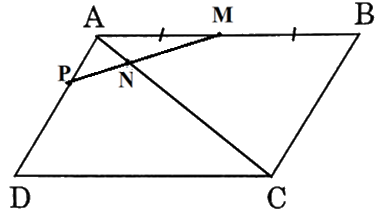
Theo giả thiết, M là trung điểm AB, N nằm giữa A và C, P nằm giữa A và D
a) Ta có:
+ \(\overrightarrow {AN} = \frac{1}{5}\overrightarrow {AC} \). Theo quy tắc hình bình hành, \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \) \( \Rightarrow \overrightarrow {AN} = \frac{1}{5}\left( {\overrightarrow {AB} + \overrightarrow {AD} } \right) = \frac{1}{5}\left( {\overrightarrow a + \overrightarrow b } \right)\)
+ \(\overrightarrow {MN} = \overrightarrow {AN} - \overrightarrow {AM} \)mà \(\overrightarrow {AN} = \frac{1}{5}\left( {\overrightarrow a + \overrightarrow b } \right)\), \(\overrightarrow {AM} = \frac{1}{2}\overrightarrow {AB} = \frac{1}{2}\overrightarrow a \)
nên \(\overrightarrow {MN} = \overrightarrow {AN} - \overrightarrow {AM} = \frac{1}{5}\left( {\overrightarrow a + \overrightarrow b } \right) - \frac{1}{2}\overrightarrow a = - \frac{3}{{10}}\overrightarrow a + \frac{1}{5}\overrightarrow b \)
+ \(\overrightarrow {NP} = \overrightarrow {AP} - \overrightarrow {AN} \) mà \(\overrightarrow {AN} = \frac{1}{5}\left( {\overrightarrow a + \overrightarrow b } \right)\), \(\overrightarrow {AP} = \frac{1}{3}\overrightarrow {AD} = \frac{1}{3}\overrightarrow b \)
nên \(\overrightarrow {NP} = \overrightarrow {AP} - \overrightarrow {AN} = \frac{1}{3}\overrightarrow b - \frac{1}{5}\left( {\overrightarrow a + \overrightarrow b } \right) = - \frac{1}{5}\overrightarrow a + \frac{2}{{15}}\overrightarrow b \)
Vậy \(\overrightarrow {AN} = \frac{1}{5}\left( {\overrightarrow a + \overrightarrow b } \right)\); \(\overrightarrow {MN} = - \frac{3}{{10}}\overrightarrow a + \frac{1}{5}\overrightarrow b \); \(\overrightarrow {NP} = - \frac{1}{5}\overrightarrow a + \frac{2}{{15}}\overrightarrow b \)
b) Theo a, \(\overrightarrow {MN} = - \frac{3}{{10}}\overrightarrow a + \frac{1}{5}\overrightarrow b \); \(\overrightarrow {NP} = - \frac{1}{5}\overrightarrow a + \frac{2}{{15}}\overrightarrow b \) \( \Rightarrow \overrightarrow {MN} = - \frac{3}{{10}}\overrightarrow a + \frac{1}{5}\overrightarrow b = \frac{3}{2}\left( { - \frac{1}{5}\overrightarrow a + \frac{2}{{15}}\overrightarrow b } \right) = \frac{3}{2}\overrightarrow {NP} \)
\( \Rightarrow \overrightarrow {MN} \) và \(\overrightarrow {NP} \) cùng phương. Vậy 3 điểm M, N, P thẳng hàng.
Bài 54 trang 100 SBT Toán 10 Cánh Diều thuộc chương trình học về vectơ trong không gian. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản về:
Bài 54 thường xoay quanh việc sử dụng vectơ để chứng minh các tính chất hình học, tìm tọa độ của các điểm, hoặc giải các bài toán liên quan đến hình học phẳng và không gian. Cụ thể, bài toán có thể yêu cầu:
Để giải bài 54 trang 100 SBT Toán 10 Cánh Diều, chúng ta sẽ tiến hành theo các bước sau:
Ví dụ minh họa (giả định bài toán yêu cầu chứng minh ba điểm A, B, C thẳng hàng):
Giả sử A(xA, yA), B(xB, yB), C(xC, yC). Để chứng minh A, B, C thẳng hàng, ta cần chứng minh vectơ AB và vectơ AC cùng phương. Điều này có nghĩa là tồn tại một số thực k khác 0 sao cho:
AB = k.AC
(xB - xA, yB - yA) = k.(xC - xA, yC - yA)
Từ đó, ta có hệ phương trình:
xB - xA = k.(xC - xA)
yB - yA = k.(yC - yA)
Giải hệ phương trình này để tìm k. Nếu tìm được k khác 0, thì A, B, C thẳng hàng.
Sau khi nắm vững phương pháp giải bài 54, các em có thể áp dụng để giải các bài tập tương tự. Một số bài tập gợi ý:
Khi giải bài tập về vectơ, các em cần lưu ý:
Bài 54 trang 100 SBT Toán 10 Cánh Diều là một bài tập quan trọng giúp các em học sinh củng cố kiến thức về vectơ và rèn luyện kỹ năng giải toán. Hy vọng với lời giải chi tiết và phương pháp giải được trình bày ở trên, các em sẽ tự tin hơn khi đối mặt với bài toán này và các bài toán tương tự.