Bài 19 trang 80 SBT Toán 10 Cánh Diều là một bài tập quan trọng trong chương trình học Toán 10, tập trung vào việc vận dụng các kiến thức về vectơ để giải quyết các bài toán hình học. Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập này, giúp các em học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Chúng tôi cung cấp không chỉ đáp án mà còn cả phương pháp giải, giúp các em hiểu rõ bản chất của bài toán và áp dụng vào các bài tập tương tự.
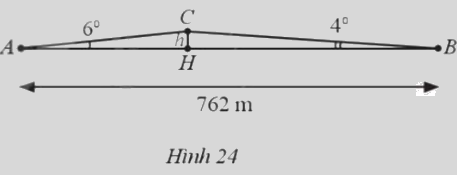
Lúc 6 giờ sáng, bạn An đi xe đạp từ nhà (điểm A) đến trường (điểm B) phải leo lên và xuống một con dốc (Hình 24). Cho biết đoạn thẳng AB dài 762 m, \(\widehat A = {6^0},\widehat B = {4^0}\)
Đề bài
Lúc 6 giờ sáng, bạn An đi xe đạp từ nhà (điểm A) đến trường (điểm B) phải leo lên và xuống một con dốc (Hình 24). Cho biết đoạn thẳng AB dài 762 m, \(\widehat A = {6^0},\widehat B = {4^0}\)
a) Tính chiều cao h của con dốc theo đơn vị mét (làm tròn kết quả đến hàng đơn vị)
b) Hỏi bạn An đến trường lúc mấy giờ? Biết rằng tốc độ trung bình lên dốc là 4 km/h và tốc độ trung bình khi xuống dốc là 19 km/h.
Phương pháp giải - Xem chi tiết
Bước 1: Tính số đo góc \(\widehat {ACB}\)và sử dụng định lí sin để tính độ dài AC hoặc BC
Bước 2: Sử dụng tỉ số lượng giác trong tam giác vuông để tính độ dài CH
Bước 3: Tính độ dài BC và thời gian đi quãng đường AC, BC để tìm thời điểm bạn An đến trường
Bước 4: Kết luận
Lời giải chi tiết
a) Ta có: \(\widehat {ACB} = {180^0} - (\widehat {CBA} + \widehat {CAB}) = {170^0}\)
Áp dụng định lí sin cho ∆ABC ta có: \(\frac{{AC}}{{\sin \widehat {CBA}}} = \frac{{AB}}{{\sin \widehat {ACB}}} \Rightarrow AC = \frac{{AB.\sin \widehat {CBA}}}{{\sin \widehat {ACB}}} = \frac{{762.\sin {4^0}}}{{\sin {{170}^0}}} \approx 306\) (m)
Xét ∆AHC vuông tại H, AC = 306 m, \(\widehat {CAH} = {6^0}\) có: \(CH = AC.\sin \widehat {CAH} = 306.\sin {6^0} \approx 32\)
Vậy chiều cao h của con dốc là 32 m
b) Áp dụng định lí sin cho ∆ABC ta có: \(\frac{{BC}}{{\sin \widehat {BAC}}} = \frac{{AB}}{{\sin \widehat {ACB}}} \Rightarrow BC = \frac{{AB.\sin \widehat {BAC}}}{{\sin \widehat {ACB}}} = \frac{{762.\sin {6^0}}}{{\sin {{170}^0}}} \approx 459\) (m)
Ta có: \(AC \approx 0,306\) km, \(BC \approx 0,459\) km
Thời gian bạn An đi quãng đường AC là \({t_1} = \frac{{0,306}}{4}\) (giờ)
Thời gian bạn An đi quãng đường AC là \({t_2} = \frac{{0,459}}{{19}}\) (giờ)
\( \Rightarrow \)Bạn An đi từ nhà đến trường hết \(t = {t_1} + {t_2} = \frac{{0,036}}{4} + \frac{{0,459}}{{19}} \approx 0,1\) giờ = 6 phút
Vậy bạn An đến trường lúc 6 giờ 6 phút.
Bài 19 trang 80 SBT Toán 10 Cánh Diều yêu cầu học sinh vận dụng kiến thức về vectơ để chứng minh các đẳng thức vectơ liên quan đến trung điểm, trọng tâm của tam giác. Để giải bài tập này một cách hiệu quả, cần nắm vững các khái niệm cơ bản về vectơ, các phép toán vectơ và các tính chất của trung điểm, trọng tâm.
Bài 19 trang 80 SBT Toán 10 Cánh Diều thường bao gồm các câu hỏi sau:
Để giải các bài tập này, ta có thể sử dụng các phương pháp sau:
Câu a: Cho tam giác ABC, tìm điểm M sao cho MA + MB + MC = 0.
Ta có: MA + MB + MC = 0. Điều này có nghĩa là M là điểm sao cho tổng các vectơ từ M đến ba đỉnh của tam giác bằng vectơ không. Điểm M thỏa mãn điều kiện này chính là trọng tâm G của tam giác ABC.
Chứng minh: Gọi G là trọng tâm của tam giác ABC. Khi đó, GA + GB + GC = 0. Do đó, M trùng với G.
Câu b: Cho tam giác ABC, gọi G là trọng tâm. Chứng minh rằng GA + GB + GC = 0.
Vì G là trọng tâm của tam giác ABC, ta có: GA = -2/3 * AD, GB = -2/3 * BE, GC = -2/3 * CF, với D, E, F lần lượt là trung điểm của BC, CA, AB.
Do đó, GA + GB + GC = -2/3 * (AD + BE + CF). Tuy nhiên, AD + BE + CF = 0 (một tính chất quen thuộc của trọng tâm). Vậy, GA + GB + GC = 0.
Câu c: Cho hình bình hành ABCD, gọi O là giao điểm của hai đường chéo. Chứng minh rằng OA + OB + OC + OD = 0.
Vì ABCD là hình bình hành, O là giao điểm của hai đường chéo AC và BD, nên O là trung điểm của AC và BD.
Do đó, OA = -OC và OB = -OD.
Vậy, OA + OB + OC + OD = OA + OB - OA - OB = 0.
Hy vọng với hướng dẫn chi tiết này, các em học sinh có thể tự tin giải bài 19 trang 80 SBT Toán 10 Cánh Diều và các bài tập tương tự. Chúc các em học tốt!