Bài 55 trang 100 SBT Toán 10 Cánh Diều là một bài tập quan trọng trong chương trình học Toán 10. Bài tập này yêu cầu học sinh vận dụng kiến thức về vectơ, các phép toán vectơ và ứng dụng của vectơ trong hình học để giải quyết các bài toán cụ thể.
Tại giaitoan.edu.vn, chúng tôi cung cấp lời giải chi tiết, dễ hiểu cho bài tập này, giúp học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Cho tam giác ABC. Lấy các điểm D, E, M, N thoả mãn \(\overrightarrow {AD} = \frac{1}{3}\overrightarrow {AB} ,\overrightarrow {AE} = \frac{2}{5}\overrightarrow {AC} ,\overrightarrow {BM} = \frac{1}{3}\overrightarrow {BC} ,\overrightarrow {AN} = k\overrightarrow {AM} \)
Đề bài
Cho tam giác ABC. Lấy các điểm D, E, M, N thoả mãn \(\overrightarrow {AD} = \frac{1}{3}\overrightarrow {AB} ,\overrightarrow {AE} = \frac{2}{5}\overrightarrow {AC} ,\overrightarrow {BM} = \frac{1}{3}\overrightarrow {BC} ,\overrightarrow {AN} = k\overrightarrow {AM} \)
với k là số thực. Biểu thị các vectơ \(\overrightarrow {AN} ,\overrightarrow {DE} ,\overrightarrow {EN} \) theo các vectơ \(\overrightarrow a = \overrightarrow {AB} ,\overrightarrow b = \overrightarrow {AC} \) và tìm k để ba điểm D, E, N thẳng hàng.
Phương pháp giải - Xem chi tiết
Bước 1: Xác định vị trí các điểm D, E, M, N trên các cạnh AB, AC, BC, AM
Bước 2: Sử dụng các quy tắc để biểu diễn các vectơ theo \(\overrightarrow {AB} \) và \(\overrightarrow {AC} \)
Bước 3: Sử dụng điều kiện \(\overrightarrow {EN} = t\overrightarrow {DE} \) chứng minh D, E, N thẳng hàng.
Lời giải chi tiết
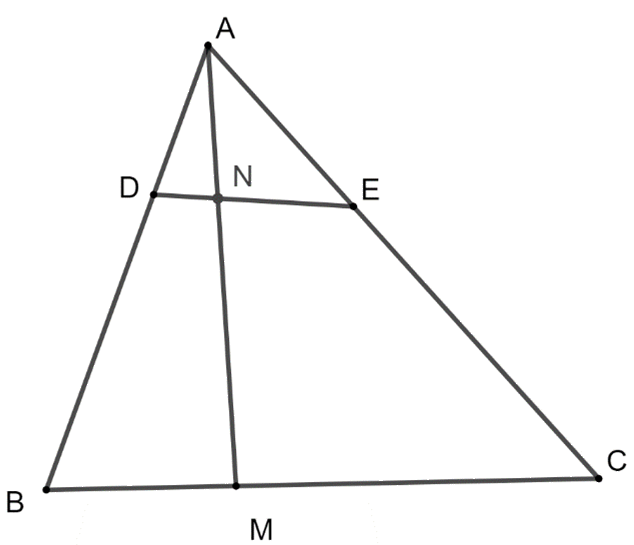
Theo giả thiết D, E, M, N nằm giữa 2 đầu mút các cạnh tương ứng AB, AC, BC, AM
a) Ta có: \(\overrightarrow {AD} = \frac{1}{3}\overrightarrow {AB} = \frac{1}{3}\overrightarrow a \); \(\overrightarrow {AE} = \frac{2}{5}\overrightarrow {AC} = \frac{2}{5}\overrightarrow b \);
\(\overrightarrow {BM} = \frac{1}{3}\overrightarrow {BC} \Leftrightarrow \overrightarrow {AM} - \overrightarrow {AB} = \frac{1}{3}\left( {\overrightarrow {AC} - \overrightarrow {AB} } \right) \Leftrightarrow \overrightarrow {AM} = \overrightarrow {AB} + \frac{1}{3}\left( {\overrightarrow {AC} - \overrightarrow {AB} } \right) \Leftrightarrow \overrightarrow {AM} = \frac{2}{3}\overrightarrow a + \frac{1}{3}\overrightarrow b \)
+ \(\overrightarrow {AN} = k\overrightarrow {AM} = k\left( {\frac{2}{3}\overrightarrow a + \frac{1}{3}\overrightarrow b } \right) = \frac{{2k}}{3}\overrightarrow a + \frac{k}{3}\overrightarrow b \)
+ \(\overrightarrow {DE} = \overrightarrow {AE} - \overrightarrow {AD} = - \frac{1}{3}\overrightarrow a + \frac{2}{5}\overrightarrow b \)
+ \(\overrightarrow {EN} = \overrightarrow {AN} - \overrightarrow {AE} = k\left( {\frac{2}{3}\overrightarrow a + \frac{1}{3}\overrightarrow b } \right) - \frac{2}{5}\overrightarrow b = \frac{{2k}}{3}\overrightarrow a + \frac{{5k - 6}}{{15}}\overrightarrow b \)
b) D, E, N thẳng hàng khi và chỉ khi \(\overrightarrow {EN} = t\overrightarrow {DE} \) \( \Leftrightarrow \frac{{2k}}{3}\overrightarrow a + \frac{{5k - 6}}{{15}}\overrightarrow b = t\left( { - \frac{1}{3}\overrightarrow a + \frac{2}{5}\overrightarrow b } \right)\)
\( \Leftrightarrow \left\{ \begin{array}{l}\frac{{2k}}{3} = - \frac{t}{3}\\\frac{{5k - 6}}{{15}} = \frac{{2t}}{5}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\frac{2}{3}k + \frac{1}{3}t = 0\\\frac{1}{3}k - \frac{2}{5}t = \frac{2}{5}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}k = \frac{6}{{17}}\\t = - \frac{{12}}{{17}}\end{array} \right.\)
Vậy với \(k = \frac{6}{{17}}\) thì D, E, N thẳng hàng.
Bài 55 trang 100 SBT Toán 10 Cánh Diều thuộc chương trình học về vectơ trong không gian. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản về vectơ, bao gồm:
Bài tập 55 thường yêu cầu học sinh thực hiện các thao tác sau:
Để giúp học sinh hiểu rõ hơn về cách giải bài tập này, chúng tôi xin trình bày lời giải chi tiết như sau:
(Ở đây sẽ là lời giải chi tiết của bài tập 55, bao gồm các bước giải, giải thích rõ ràng và các lưu ý quan trọng. Lời giải sẽ được trình bày một cách logic và dễ hiểu, sử dụng các ký hiệu toán học chính xác.)
Để minh họa cho phương pháp giải bài tập này, chúng ta hãy xem xét một ví dụ cụ thể:
(Ở đây sẽ là một ví dụ tương tự bài 55, được giải chi tiết để học sinh có thể tham khảo và áp dụng vào các bài tập khác.)
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập về vectơ, học sinh có thể tham khảo các bài tập tương tự sau:
Khi giải bài tập về vectơ, học sinh cần lưu ý những điều sau:
Bài 55 trang 100 SBT Toán 10 Cánh Diều là một bài tập quan trọng giúp học sinh củng cố kiến thức về vectơ và rèn luyện kỹ năng giải bài tập. Hy vọng với lời giải chi tiết và các lưu ý trên, học sinh có thể tự tin giải bài tập này và đạt kết quả tốt trong môn Toán 10.
| Khái niệm | Giải thích |
|---|---|
| Vectơ | Một đoạn thẳng có hướng, xác định bởi điểm gốc và điểm cuối. |
| Tích vô hướng | Một phép toán giữa hai vectơ, cho ra một số thực. |