Bài 51 trang 62 SBT Toán 10 Cánh Diều là một bài tập quan trọng trong chương trình học Toán 10. Bài tập này yêu cầu học sinh vận dụng kiến thức về vectơ, các phép toán vectơ và ứng dụng của vectơ trong hình học để giải quyết các bài toán cụ thể.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 51 trang 62 SBT Toán 10 Cánh Diều, giúp các em học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Giải các bất phương trình bậc hai sau:
Đề bài
Giải các bất phương trình bậc hai sau:
a) \(4{x^2} - 9x + 5 \le 0\)
b) \( - 3{x^2} - x + 4 > 0\)
c) \(36{x^2} - 12x + 1 > 0\)
d) \( - 7{x^2} + 5x + 2 < 0\)
Phương pháp giải - Xem chi tiết
Sử dụng định lý về dấu của tam thức bậc hai
Bước 1: Xác định dấu của hệ số \(a\) và tìm nghiệm của \(f\left( x \right)\) (nếu có)
Bước 2: Sử dụng định lý về dấu của tam thức bậc hai để tìm tập hợp các giá trị của của x sao cho \(f\left( x \right)\) mang dấu thỏa mãn bất phương trình
+ Nếu \(\Delta < 0\) thì \(f\left( x \right)\) cùng dấu với hệ số \(a\) với mọi \(x \in \mathbb{R}\)
+ Nếu \(\Delta = 0\) thì \(f\left( x \right)\) cùng dấu với hệ số \(a\) với mọi \(x \in \mathbb{R}\backslash \left\{ {\frac{{ - b}}{{2a}}} \right\}\)
+ Nếu \(\Delta > 0\) thì \(f\left( x \right)\) có hai nghiệm \({x_1},{x_2}\left( {{x_1} < {x_2}} \right)\). Khi đó:
\(f\left( x \right)\) cùng dấu với hệ số \(a\) với mọi \(x\) thuộc các khoảng \(\left( { - \infty ;{x_1}} \right) \cup \left( {{x_2}; + \infty } \right)\)
\(f\left( x \right)\) trái dấu với hệ số \(a\) với mọi \(x\) thuộc khoảng \(\left( {x{ & _1};{x_2}} \right)\)
Lời giải chi tiết
a) \(4{x^2} - 9x + 5 \le 0\)
Tam thức bậc hai \(4{x^2} - 9x + 5\) có hai nghiệm \({x_1} = 1;{x_2} = \frac{5}{4}\) và có hệ số \(a = 4 > 0\)
Sử dụng định lý về dấu của tam thức bậc hai

Ta thấy tập hợp những giá trị của \(x\) sao cho tam thức \(4{x^2} - 9x + 5\) mang dấu “-” là \(\left[ {1;\frac{5}{4}} \right]\)
b) \( - 3{x^2} - x + 4 > 0\)
Tam thức bậc hai \( - 3{x^2} - x + 4\) có hai nghiệm \({x_1} = - \frac{4}{3};{x_2} = 1\) và có hệ số \(a = - 3 < 0\)
Sử dụng định lý về dấu của tam thức bậc hai

Ta thấy tập hợp những giá trị của \(x\) sao cho tam thức \( - 3{x^2} - x + 4\) mang dấu “+” là \(\left( { - \frac{4}{3};1} \right)\)
c) \(36{x^2} - 12x + 1 > 0\)
Tam thức bậc hai \(36{x^2} - 12x + 1\) có nghiệm kép \({x_0} = \frac{1}{6}\) và có hệ số \(a = 36 > 0\)
Sử dụng định lý về dấu của tam thức bậc hai, ta thấy tập hợp những giá trị của \(x\) sao cho tam thức \(36{x^2} - 12x + 1\) mang dấu “+” là \(\mathbb{R}\backslash \left\{ {\frac{1}{6}} \right\}\)
d) \( - 7{x^2} + 5x + 2 < 0\)
Tam thức bậc hai \( - 7{x^2} + 5x + 2\) có hai nghiệm \({x_1} = \frac{{ - 2}}{7};{x_2} = 1\) và có hệ số \(a = - 7 < 0\)
Sử dụng định lý về dấu của tam thức bậc hai
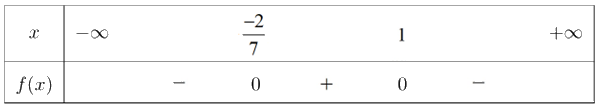
Ta thấy tập hợp những giá trị của \(x\) sao cho tam thức \( - 7{x^2} + 5x + 2\) mang dấu “-” là \(\left( { - \infty ;\frac{{ - 2}}{7}} \right) \cup \left( {1; + \infty } \right)\)
Bài 51 trang 62 SBT Toán 10 Cánh Diều thuộc chương trình học về vectơ trong không gian. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản về vectơ, bao gồm:
Bài 51 thường yêu cầu học sinh:
Để cung cấp lời giải chi tiết, chúng ta cần xem xét nội dung cụ thể của bài toán. Giả sử bài toán yêu cầu:
Cho hình hộp ABCD.A'B'C'D'. Gọi M là trung điểm của cạnh AB. Chứng minh rằng: vectơ AM = 1/2 vectơ AB.
Lời giải:
Vì M là trung điểm của cạnh AB, theo định nghĩa trung điểm, ta có:
vectơ AM = vectơ MB
Mà vectơ AB = vectơ AM + vectơ MB
Suy ra vectơ AB = vectơ AM + vectơ AM = 2vectơ AM
Do đó, vectơ AM = 1/2 vectơ AB (đpcm)
Ngoài bài 51, SBT Toán 10 Cánh Diều còn có nhiều bài tập tương tự về vectơ. Để giải quyết các bài tập này, học sinh có thể áp dụng các phương pháp sau:
Để củng cố kiến thức và kỹ năng giải bài tập về vectơ, học sinh nên luyện tập thêm các bài tập sau:
Bài 51 trang 62 SBT Toán 10 Cánh Diều là một bài tập quan trọng giúp học sinh hiểu sâu hơn về vectơ và ứng dụng của vectơ trong hình học. Bằng cách nắm vững các khái niệm cơ bản, áp dụng các phương pháp giải phù hợp và luyện tập thường xuyên, học sinh có thể giải quyết bài tập này một cách dễ dàng và hiệu quả.
Giaitoan.edu.vn hy vọng rằng lời giải chi tiết và các hướng dẫn trên sẽ giúp các em học sinh học tốt môn Toán 10.