Bài 29 trang 73 SBT Toán 10 Cánh Diều là một bài tập quan trọng trong chương trình học Toán 10. Bài tập này yêu cầu học sinh vận dụng kiến thức về vectơ, các phép toán vectơ và ứng dụng của vectơ trong hình học để giải quyết các bài toán cụ thể.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 29 trang 73 SBT Toán 10 Cánh Diều, giúp các em học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Cho tam giác ABC, biết toạ độ trung điểm các cạnh BC, CA, AB lần lượt là M(-1 ; 1), N(3 ; 4), P(5 ; 6).
Đề bài
Cho tam giác ABC, biết toạ độ trung điểm các cạnh BC, CA, AB lần lượt là M(-1 ; 1), N(3 ; 4), P(5 ; 6).
a) Viết phương trình tham số của các đường thẳng AB, BC, CA
b) Viết phương trình tổng quát của các đường trung trực của tam giác ABC
Phương pháp giải - Xem chi tiết
Bước 1: Tìm tọa độ các vectơ \(\overrightarrow {MN} ,\overrightarrow {MP} ,\overrightarrow {NP} \) rồi xác định các VTCP của AB, BC, CA
Bước 2: Viết PT tham số của các đường thẳng AB, BC, CA khi biết điểm đi qua và VTCP
Bước 3: Tìm các VTPT của các đường trung trực của ∆ABC là các vectơ \(\overrightarrow {MN} ,\overrightarrow {MP} ,\overrightarrow {NP} \)
Bước 4: Viết PTTQ các đường trung trực của tam giác ABC
Lời giải chi tiết
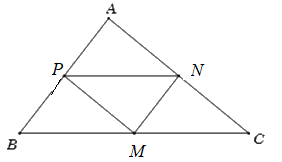
a) Theo giả thiết, MN, MP, NP là các đường trung bình của ∆ABC \( \Rightarrow MN//AB,MP//AC,NP//BC\)
Khi đó, AB, AC, BC lần lượt nhận các vectơ \(\overrightarrow {MN} = (4;3),\overrightarrow {MP} = (6;5),\overrightarrow {NP} = (2;2)\) làm VTCP
+ AB đi qua P, nhận \(\overrightarrow {MN} = (4;3)\) làm VTCP nên có PT tham số: \(\left\{ \begin{array}{l}x = 5 + 4t\\y = 6 + 3t\end{array} \right.\)
+ AC đi qua N, nhận \(\overrightarrow {MP} = (6;5)\) làm VTCP nên có PT tham số: \(\left\{ \begin{array}{l}x = 3 + 6k\\y = 4 + 5k\end{array} \right.\)
+ BC đi qua M, nhận \(\overrightarrow u = (1;1)\)cùng phương với \(\overrightarrow {NP} = (2;2)\) làm VTCP nên có PT tham số:
\(\left\{ \begin{array}{l}x = - 1 + p\\y = 1 + p\end{array} \right.\)
b) Ta có:
+ Đường trung trực của cạnh AB đi qua P và nhận \(\overrightarrow {MN} = (4;3)\) làm VTPT nên có PTTQ:
4x + 3y – 38 = 0
+ Đường trung trực của cạnh AC đi qua N và nhận \(\overrightarrow {MP} = (6;5)\) làm VTPT nên có PTTQ:
6x + 5y – 38 = 0
+ Đường trung trực của cạnh BC đi qua M và nhận \(\overrightarrow {NP} = (2;2)\) làm VTPT nên có PTTQ:
2x + 2y = 0 \( \Leftrightarrow x + y = 0\)
Bài 29 trang 73 SBT Toán 10 Cánh Diều thuộc chương trình học về vectơ trong không gian. Bài tập này thường tập trung vào việc xác định tọa độ của vectơ, thực hiện các phép toán cộng, trừ, nhân với một số thực, và tính độ dài của vectơ. Để giải quyết bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản về vectơ, các công thức liên quan và kỹ năng áp dụng vào thực tế.
Bài 29 thường bao gồm các dạng bài tập sau:
Để giúp học sinh hiểu rõ hơn về cách giải bài 29 trang 73 SBT Toán 10 Cánh Diều, chúng ta sẽ đi vào giải chi tiết từng phần của bài tập. (Ở đây sẽ là nội dung giải chi tiết từng câu hỏi của bài 29, giả sử bài 29 có 3 câu a, b, c. Mỗi câu sẽ được trình bày chi tiết với các bước giải rõ ràng, kèm theo giải thích lý thuyết liên quan.)
Đề bài: Cho A(1; 2) và B(3; 4). Tìm tọa độ của vectơ AB.
Giải:
Vectơ AB có tọa độ là (xB - xA; yB - yA) = (3 - 1; 4 - 2) = (2; 2).
Vậy, tọa độ của vectơ AB là (2; 2).
Vectơ là một công cụ mạnh mẽ trong việc giải quyết các bài toán hình học. Nó giúp chúng ta biểu diễn các đại lượng hình học một cách chính xác và dễ dàng thao tác. Việc nắm vững kiến thức về vectơ sẽ giúp học sinh giải quyết các bài toán hình học một cách hiệu quả hơn.
Để củng cố kiến thức về vectơ và rèn luyện kỹ năng giải toán, học sinh có thể tham khảo các bài tập sau:
Bài 29 trang 73 SBT Toán 10 Cánh Diều là một bài tập quan trọng giúp học sinh nắm vững kiến thức về vectơ và ứng dụng của nó trong hình học. Hy vọng với lời giải chi tiết và các lưu ý quan trọng mà Giaitoan.edu.vn cung cấp, các em học sinh sẽ tự tin hơn trong việc giải quyết các bài tập tương tự.