Giải bài 16 trang 38 Sách bài tập Toán 10 - Cánh Diều

Giải bài 16 trang 38 sách bài tập toán 10 - Cánh diều

Giải bài 16 trang 38 Sách bài tập Toán 10 - Cánh Diều

Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho bài 16 trang 38 sách bài tập Toán 10 chương trình Cánh Diều. Bài viết này sẽ giúp bạn nắm vững kiến thức và kỹ năng giải toán, tự tin hơn trong các bài kiểm tra.

Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn lời giải bài 16 trang 38 một cách cẩn thận, đảm bảo tính chính xác và dễ tiếp thu.

Biểu đồ đoạn thẳng ở Hình 3 biểu diễn số lượt khách vào một cửa hàng trong ngày đầu khai trương tại một số mốc thời gian.

Đề bài

Biểu đồ đoạn thẳng ở Hình 3 biểu diễn số lượt khách vào một cửa hàng trong ngày đầu khai trương tại một số mốc thời gian.

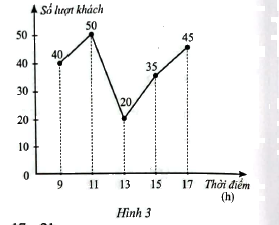
Giải bài 16 trang 38 sách bài tập toán 10 - Cánh diều 1

Mẫu số liệu nhận được từ biểu đồ ở Hình 3 có khoảng tứ phân vị là bao nhiêu?

A. 10 B. 15 C. 20 D. 5

Phương pháp giải - Xem chi tiết Giải bài 16 trang 38 sách bài tập toán 10 - Cánh diều 2

+ Khoảng tứ phân vị: \(\Delta Q = {Q_3} - {Q_1}\)

Bước 1: Sắp xếp các số liệu theo thứ tự không giảm.

Bước 2: Tính cỡ mẫu \(n\), tìm tứ phân vị thứ hai \({Q_2}\)(chính là trung vị của mẫu).

Bước 3: Tìm tứ phân vị thứ nhất: là trung vị của nửa số liệu đã sắp xếp bên trái \({Q_2}\) (không bao gồm \({Q_2}\) nếu n lẻ)

Bước 4: Tìm tứ phân vị thứ ba: là trung vị của nửa số liệu đã sắp xếp bên phải \({Q_2}\) (không bao gồm \({Q_2}\) nếu n lẻ)

Lời giải chi tiết

+ Sắp xếp mẫu số liệu theo thứ tự không giảm ta được: \(20;35;40;45;50\)

+ Vì \(n = 5\) là số lẻ nên tứ phân vị thứ hai là: \({Q_2} = 40\) là tứ phân vị

+ Tứ phân vị thứ nhất là trung vị của 2 số đầu tiên của mẫu số liệu: \({Q_1} = \left( {20 + 35} \right):2 = 27,5\)

+ Tứ phân vị thứ ba là trung vị của 2 số cuối của mẫu số liệu: \({Q_3} = \left( {45 + 50} \right):2 = 47,5\)

+ Khoảng tứ phân vị: \(\Delta Q = {Q_3} - {Q_1} = 47,5 - 27,5 = 20\)

Chọn C.

Xây dựng nền tảng Toán THPT vững vàng từ hôm nay! Đừng bỏ lỡ Giải bài 16 trang 38 sách bài tập toán 10 - Cánh diều đặc sắc thuộc chuyên mục học toán 10 trên nền tảng môn toán. Với bộ bài tập toán thpt được biên soạn chuyên sâu, bám sát chương trình Toán lớp 10, đây chính là "kim chỉ nam" giúp các em tối ưu hóa ôn luyện, củng cố kiến thức cốt lõi và chuẩn bị hành trang vững chắc cho tương lai. Phương pháp học trực quan, logic sẽ mang lại hiệu quả vượt trội trên lộ trình chinh phục đại học!

Giải bài 16 trang 38 Sách bài tập Toán 10 - Cánh Diều: Phương pháp tiếp cận chi tiết

Bài 16 trang 38 sách bài tập Toán 10 Cánh Diều thuộc chương trình học về hàm số bậc hai. Để giải quyết bài toán này một cách hiệu quả, chúng ta cần nắm vững các kiến thức cơ bản về:

Định nghĩa hàm số bậc hai: Hàm số có dạng y = ax² + bx + c, với a ≠ 0.
Đồ thị hàm số bậc hai (Parabol): Hình dạng, đỉnh, trục đối xứng, giao điểm với các trục tọa độ.
Các yếu tố ảnh hưởng đến đồ thị: Hệ số a, b, c.
Ứng dụng của hàm số bậc hai: Giải các bài toán thực tế.

Nội dung bài 16: Bài 16 thường tập trung vào việc xác định các yếu tố của parabol (đỉnh, trục đối xứng, giao điểm) dựa trên phương trình hàm số bậc hai. Đôi khi, bài toán yêu cầu vẽ đồ thị hàm số hoặc tìm các điểm thuộc đồ thị.

Hướng dẫn giải chi tiết bài 16 trang 38

Để giải bài 16 trang 38, chúng ta sẽ thực hiện theo các bước sau:

Xác định hệ số a, b, c: Từ phương trình hàm số bậc hai, xác định chính xác giá trị của a, b, c.
Tính tọa độ đỉnh của parabol: Sử dụng công thức x_đỉnh = -b/2a và y_đỉnh = f(x_đỉnh).
Xác định trục đối xứng: Trục đối xứng của parabol là đường thẳng x = x_đỉnh.
Tìm giao điểm với trục Oy: Giao điểm với trục Oy là điểm có tọa độ (0, c).
Tìm giao điểm với trục Ox (nếu có): Giải phương trình ax² + bx + c = 0 để tìm các nghiệm x. Các nghiệm này là hoành độ của các giao điểm với trục Ox.
Vẽ đồ thị hàm số: Dựa vào các thông tin đã tính toán, vẽ đồ thị hàm số trên hệ trục tọa độ.

Ví dụ minh họa

Giả sử chúng ta có hàm số y = x² - 4x + 3. Hãy giải bài 16 trang 38 với hàm số này:

Hệ số: a = 1, b = -4, c = 3.
Đỉnh: x_đỉnh = -(-4)/(2*1) = 2; y_đỉnh = 2² - 4*2 + 3 = -1. Vậy đỉnh của parabol là (2, -1).
Trục đối xứng: x = 2.
Giao điểm với trục Oy: (0, 3).
Giao điểm với trục Ox: Giải phương trình x² - 4x + 3 = 0, ta được x₁ = 1 và x₂ = 3. Vậy giao điểm với trục Ox là (1, 0) và (3, 0).

Dựa vào các thông tin này, bạn có thể vẽ đồ thị hàm số y = x² - 4x + 3.

Lưu ý quan trọng

Khi giải bài 16 trang 38, bạn cần chú ý:

Kiểm tra kỹ các hệ số a, b, c: Sai sót trong việc xác định hệ số có thể dẫn đến kết quả sai.
Sử dụng đúng công thức: Đảm bảo bạn áp dụng đúng các công thức tính toán.
Vẽ đồ thị chính xác: Đồ thị hàm số phải thể hiện đúng các yếu tố đã tính toán.

Các dạng bài tập tương tự:

Tìm tọa độ đỉnh, trục đối xứng, giao điểm của các hàm số bậc hai khác.
Xác định phương trình hàm số bậc hai khi biết các yếu tố của parabol.
Giải các bài toán ứng dụng liên quan đến hàm số bậc hai.

Giaitoan.edu.vn hy vọng rằng hướng dẫn chi tiết này sẽ giúp bạn giải bài 16 trang 38 sách bài tập Toán 10 Cánh Diều một cách dễ dàng và hiệu quả. Chúc bạn học tập tốt!