Bài 11 trang 75 SBT Toán 10 Cánh Diều là một bài tập quan trọng trong chương trình học Toán 10. Bài tập này yêu cầu học sinh vận dụng kiến thức về vectơ, các phép toán vectơ và ứng dụng của vectơ trong hình học để giải quyết các bài toán cụ thể.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 11 trang 75 SBT Toán 10 Cánh Diều, giúp các em học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Tàu A cách cảng C một khoảng 3 km và lệch hướng bắc một góc 47,450.
Đề bài
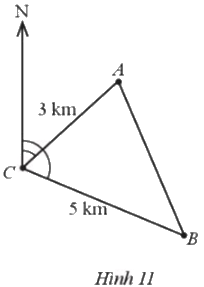
Tàu A cách cảng C một khoảng 3 km và lệch hướng bắc một góc 47,450. Tàu B cách cảng C một khoảng 5 km và lệch hướng bắc một góc 112,900 (Hình 11). Hỏi khoảng cách giữa hai tàu là bao nhiêu kilomet (làm tròn kết quả đến hàng phần trăm)?
Phương pháp giải - Xem chi tiết
Bước 1: Từ giả thiết xác định số đo các góc \(\widehat {NCA},\widehat {NCB},\widehat {ACB}\)
Bước 2: Áp dụng định lí cosin cho ∆ABC để tính độ dài AB rồi kết luận
Lời giải chi tiết
Theo giả thiết,
\(\widehat {NCA} = 47,{45^0},\widehat {NCB} = 112,{90^0} \Rightarrow \widehat {ACB} = \widehat {NCB} - \widehat {NCA} = 65,{45^0}\)
Áp dụng định lí cosin cho ∆ABC ta có:
\(A{B^2} = A{C^2} + B{C^2} - 2.AC.BC.\cos \widehat {ACB}\)
\( \Rightarrow AB = \sqrt {A{C^2} + B{C^2} - 2.AC.BC.\cos \widehat {ACB}} \)
\( = \sqrt {{3^2} + {5^2} - 2.3.5.\cos 65,{{45}^0}} \approx 4,64\)
Vậy khoảng cách giữa hai tàu là 4,64 km
Bài 11 trang 75 SBT Toán 10 Cánh Diều thuộc chương trình học về vectơ trong không gian. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản về:
Bài tập 11 thường xoay quanh việc sử dụng vectơ để chứng minh các tính chất hình học, tìm tọa độ của các điểm, hoặc giải các bài toán liên quan đến hình học phẳng và không gian. Cụ thể, bài tập có thể yêu cầu:
Để giúp các em học sinh hiểu rõ hơn về cách giải bài tập này, chúng ta sẽ đi vào phân tích từng phần của bài tập và đưa ra lời giải chi tiết.
Trước khi bắt đầu giải bài tập, điều quan trọng là phải đọc kỹ đề bài và xác định rõ yêu cầu của bài toán. Xác định các yếu tố đã cho và các yếu tố cần tìm. Vẽ hình minh họa (nếu cần thiết) để giúp hình dung rõ hơn về bài toán.
Sau khi đã phân tích đề bài, chúng ta sẽ áp dụng các kiến thức và công thức đã học để giải quyết bài toán. Lựa chọn phương pháp giải phù hợp với từng dạng bài tập. Ví dụ, nếu bài tập yêu cầu chứng minh hai vectơ cùng phương, chúng ta có thể sử dụng định nghĩa hai vectơ cùng phương hoặc kiểm tra xem hai vectơ có cùng hướng và tỷ lệ hay không.
Trình bày lời giải một cách rõ ràng, logic và dễ hiểu. Viết đầy đủ các bước giải và giải thích rõ ràng các bước đó. Sử dụng các ký hiệu toán học chính xác và tránh sử dụng các ngôn ngữ không rõ ràng.
Đề bài: Cho tam giác ABC. Gọi M là trung điểm của BC. Chứng minh rằng overrightarrow{AM} = (overrightarrow{AB} +overrightarrow{AC})/2.
Lời giải:
Để củng cố kiến thức và rèn luyện kỹ năng giải toán, các em học sinh nên luyện tập thêm các bài tập tương tự. Các bài tập này có thể tìm thấy trong sách bài tập Toán 10 Cánh Diều hoặc trên các trang web học toán online.
Bài 11 trang 75 SBT Toán 10 Cánh Diều là một bài tập quan trọng giúp học sinh hiểu sâu hơn về vectơ và ứng dụng của vectơ trong hình học. Hy vọng rằng với lời giải chi tiết và các lời khuyên trên, các em học sinh sẽ giải quyết bài tập này một cách dễ dàng và hiệu quả.