Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 10. Bài viết này sẽ hướng dẫn bạn giải bài 43 trang 92 SBT Toán 10 - Cánh Diều một cách nhanh chóng và hiệu quả.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, giúp bạn tự tin hơn trong việc chinh phục môn Toán.
Cho tứ giác ABCD là hình bình hành. Gọi O là giao điểm của hai đường chéo , E là trung điểm của AD, G là giao điểm của BE và AC. Tính:
Đề bài
Cho tứ giác ABCD là hình bình hành. Gọi O là giao điểm của hai đường chéo , E là trung điểm của AD, G là giao điểm của BE và AC. Tính:
a) \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} \)
b) \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GD} \)
Phương pháp giải - Xem chi tiết
Bước 1: Sử dụng tính chất O là trung điểm AC, BD để tính \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} \)
Bước 2: Chứng minh G là trọng tâm tam giác ABD rồi tính \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GD} \)
Lời giải chi tiết
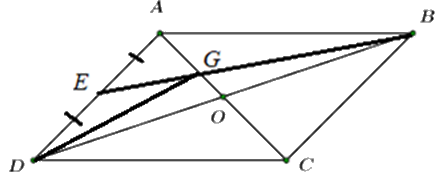
a) Do ABCD là hình bình hành nên O là trung điểm AC và BD
\( \Rightarrow \overrightarrow {OA} + \overrightarrow {OC} = \overrightarrow 0 ,\overrightarrow {OB} + \overrightarrow {OD} = \overrightarrow 0 \) \(\begin{array}{l} \Rightarrow \overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OC} + \overrightarrow {OD} = \left( {\overrightarrow {OA} + \overrightarrow {OC} } \right) + \left( {\overrightarrow {OB} + \overrightarrow {OD} } \right)\\ = \overrightarrow 0 + \overrightarrow 0 = \overrightarrow 0 \end{array}\)
b) Xét tam giác ABD có AO và BE là hai đường trung tuyến cắt nhau tại G
\( \Rightarrow \) G là trọng tâm ∆ABD \( \Rightarrow \overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GD} = \overrightarrow 0 \)
Bài 43 trang 92 SBT Toán 10 - Cánh Diều thuộc chương trình học Toán 10, tập trung vào việc vận dụng các kiến thức về vectơ, phép toán vectơ, và các ứng dụng của vectơ trong hình học. Bài tập này thường yêu cầu học sinh phải hiểu rõ định nghĩa, tính chất của vectơ, cũng như các quy tắc cộng, trừ, nhân vectơ với một số thực.
Bài 43 thường bao gồm các dạng bài tập sau:
Để giúp các bạn học sinh hiểu rõ hơn về cách giải bài 43 trang 92 SBT Toán 10 - Cánh Diều, chúng tôi sẽ trình bày lời giải chi tiết cho từng câu hỏi trong bài tập.
Đề bài: (Giả định đề bài cụ thể ở đây)
Lời giải: (Giải thích chi tiết từng bước, sử dụng công thức và định lý liên quan. Ví dụ:)
Gọi A, B, C là các điểm có tọa độ A(xA, yA), B(xB, yB), C(xC, yC). Khi đó, vectơ AB có tọa độ (xB - xA, yB - yA). Áp dụng công thức này, ta tính được tọa độ của vectơ AB, BC, CA. Sau đó, ta kiểm tra xem vectơ AB có cùng phương với vectơ BC hay không bằng cách xét tỉ số giữa các tọa độ tương ứng. Nếu tỉ số này bằng nhau, thì ba điểm A, B, C thẳng hàng.
Đề bài: (Giả định đề bài cụ thể ở đây)
Lời giải: (Giải thích chi tiết từng bước, sử dụng công thức và định lý liên quan)
Đề bài: (Giả định đề bài cụ thể ở đây)
Lời giải: (Giải thích chi tiết từng bước, sử dụng công thức và định lý liên quan)
Để giải các bài tập về vectơ một cách hiệu quả, bạn nên:
Vectơ là một công cụ mạnh mẽ trong hình học, được sử dụng để:
Để củng cố kiến thức về vectơ, bạn có thể làm thêm các bài tập tương tự sau:
Hy vọng rằng, với lời giải chi tiết và những hướng dẫn trên, bạn đã có thể giải bài 43 trang 92 SBT Toán 10 - Cánh Diều một cách dễ dàng và hiệu quả. Chúc bạn học tốt môn Toán!