Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho bài 32 trang 16 sách bài tập Toán 10 chương trình Cánh Diều. Bài viết này sẽ giúp bạn nắm vững kiến thức và kỹ năng giải toán, tự tin hơn trong các bài kiểm tra.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn lời giải bài 32 trang 16 một cách cẩn thận, đảm bảo tính chính xác và dễ tiếp thu.
Khai triển các biểu thức sau:
Đề bài
Khai triển các biểu thức sau:
a) \({(4x + 1)^4}\) b) \({(5x - 3)^4}\) c) \({\left( {\frac{1}{3}x + 5} \right)^5}\) d) \({\left( {3x - \frac{1}{3}} \right)^5}\)
Phương pháp giải - Xem chi tiết
Áp dụng các công thức khai triển:
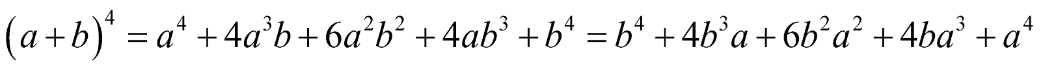
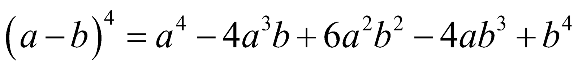
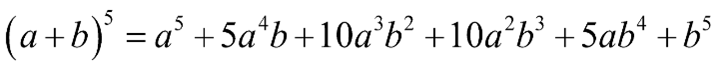
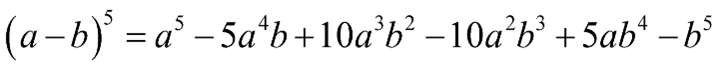
Lời giải chi tiết
a) Ta có:
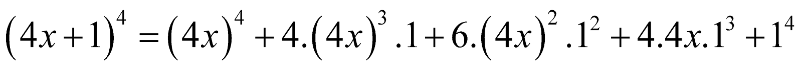
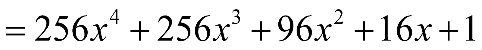
b) Ta có:
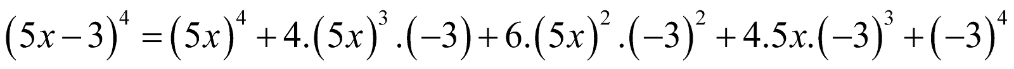
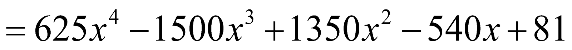
c) Ta có:
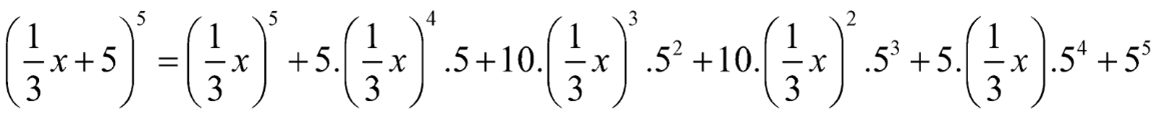
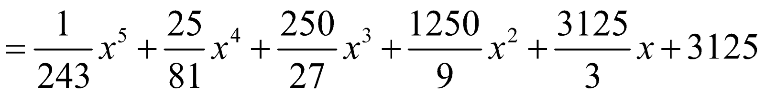
d) Ta có:
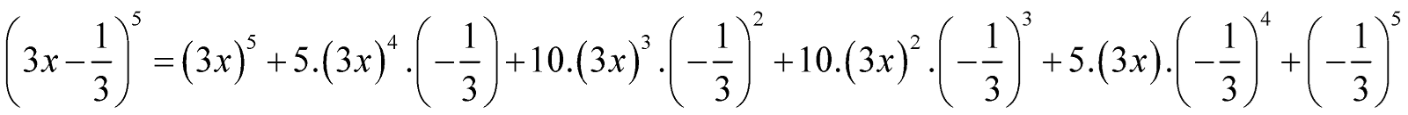
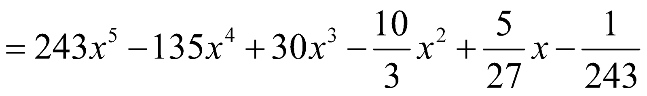
Bài 32 trang 16 sách bài tập Toán 10 Cánh Diều thuộc chương trình học về hàm số bậc hai. Để giải bài tập này một cách hiệu quả, trước hết chúng ta cần nắm vững các khái niệm cơ bản về hàm số bậc hai, bao gồm:
Nội dung bài 32: Bài 32 thường yêu cầu học sinh xác định các yếu tố của parabol (đỉnh, trục đối xứng, hệ số a) từ phương trình hàm số, hoặc ngược lại, viết phương trình parabol khi biết các yếu tố này. Ngoài ra, bài tập có thể yêu cầu tìm giá trị của hàm số tại một điểm cho trước, hoặc giải các bài toán liên quan đến ứng dụng của hàm số bậc hai.
Để giải bài 32 trang 16 sách bài tập Toán 10 Cánh Diều, chúng ta sẽ tiến hành theo các bước sau:
Ví dụ minh họa:
Giả sử bài 32 yêu cầu xác định các yếu tố của parabol có phương trình y = 2x2 - 4x + 1.
Giải:
Ngoài việc xác định các yếu tố của parabol, bài 32 trang 16 sách bài tập Toán 10 Cánh Diều còn có thể xuất hiện các dạng bài tập sau:
Để giải các bài toán ứng dụng, cần đọc kỹ đề bài, xác định các yếu tố liên quan đến hàm số bậc hai, và xây dựng phương trình toán học phù hợp. Sau đó, giải phương trình để tìm ra kết quả.
Khi giải bài tập về hàm số bậc hai, cần lưu ý những điều sau:
Hy vọng với hướng dẫn chi tiết này, bạn sẽ tự tin giải bài 32 trang 16 sách bài tập Toán 10 Cánh Diều một cách hiệu quả. Chúc bạn học tập tốt!