Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 35 trang 15 Sách bài tập Toán 10 - Cánh Diều. Bài viết này sẽ cung cấp đáp án chính xác, phương pháp giải rõ ràng, giúp các em học sinh hiểu sâu kiến thức và tự tin làm bài tập.
Chúng tôi luôn cố gắng mang đến những tài liệu học tập chất lượng, hỗ trợ tối đa cho quá trình học tập của các em. Hãy cùng theo dõi bài giải dưới đây để nắm vững kiến thức Toán 10 nhé!
Lớp 10A có 27 học sinh tham gia ít nhất một trong hai câu lạc bộ bóng đá và cờ vua, trong đó có 19 học sinh tham gia câu lạc bộ bóng đá, 15 học sinh tham gia câu lạc bộ cờ vua.
Đề bài
Lớp 10A có 27 học sinh tham gia ít nhất một trong hai câu lạc bộ bóng đá và cờ vua, trong đó có 19 học sinh tham gia câu lạc bộ bóng đá, 15 học sinh tham gia câu lạc bộ cờ vua.
a) Có bao nhiêu học sinh tham gia câu lạc bộ bóng đá mà không tham gia câu lạc bộ cờ vua?
b) Có bao nhiêu học sinh tham gia cả hai câu lạc bộ?
c) Biết trong lớp có 8 học sinh không tham gia câu lạc bộ nào trong hai câu lạc bộ trên. Lớp 10A có bao nhiêu học sinh?
Lời giải chi tiết
Gọi A là tập hợp các học sinh tham gia câu lạc bộ bóng đá,
B là tập hợp các học sinh tham gia câu lạc bộ cờ vua.
\( \Rightarrow A \cup B\) là tập hợp các học sinh tham gia ít nhất một trong hai câu lạc bộ bóng đá và cờ vua
\(A \cap B\) là tập hợp các học sinh tham gia cả hai câu lạc bộ
a) Ta có: \(n\left( A \right) = 19,{\rm{ }}n\left( B \right) = 15,n(A \cup B) = 27\)
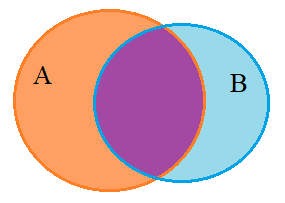
Tập hợp học sinh tham gia câu lạc bộ bóng đá mà không tham gia câu lạc bộ cờ vua là tập A\B (phần màu cam) hay chính là tập hợp \((A \cup B)\backslash B\)
Số phần tử của tập hợp \((A \cup B)\backslash B\) là số học sinh tham gia một trong hai câu lạc bộ trừ đi số học sinh tham gia câu lạc bộ cờ vua.
\(n((A \cup B)\backslash B) = n(A \cup B)--n\left( B \right) = 27--15 = 12.\)
Vậy số học sinh tham gia câu lạc bộ bóng đá mà không tham gia câu lạc bộ cờ vua là 12 học sinh.
b) Tập hợp số học sinh tham gia cả hai câu lạc bộ là tập \(A \cap B\).
Số phần tử của tập hợp \(A \cap B\)bằng số học sinh tham gia câu lạc bộ bóng đá trừ đi số học sinh chỉ tham gia câu lạc bộ bóng đá mà không tham gia câu lạc bộ cờ vua.
\( \Rightarrow n(A \cap B) = n\left( A \right)--n(A{\rm{\backslash }}B) = 19--12 = 7.\)
Vậy số học sinh tham gia cả hai câu lạc bộ là 7 học sinh
c) Lớp 10A gồm các học sinh tham gia ít nhất một trong hai câu lạc bộ và các học sinh không tham gia câu lạc bộ nào.
=> số học sinh của lớp 10A là: 27 + 8 = 35 (học sinh)
Vậy số học sinh của lớp 10A là 35 học sinh.
Bài 35 trang 15 Sách bài tập Toán 10 - Cánh Diều thuộc chương trình học Toán 10, tập trung vào việc vận dụng các kiến thức về vectơ, phép toán vectơ, và các ứng dụng của vectơ trong hình học. Bài tập này thường yêu cầu học sinh phải hiểu rõ định nghĩa, tính chất của vectơ, cũng như các quy tắc cộng, trừ, nhân vectơ với một số thực.
Bài 35 bao gồm một số câu hỏi và bài tập khác nhau, yêu cầu học sinh:
Để giải bài 35 trang 15 Sách bài tập Toán 10 - Cánh Diều một cách hiệu quả, các em cần:
Ví dụ 1: Cho tam giác ABC. Gọi M là trung điểm của BC. Chứng minh rằng AB + AC = 2AM.
Giải:
Vì M là trung điểm của BC, ta có BM = MC. Do đó, BC = 2BM.
Áp dụng quy tắc cộng vectơ, ta có:
AB + AC = AB + (AM + MC) = AB + AM + MC
Vì BM = MC, ta có BC = 2BM = 2MC.
Do đó, AB + AC = AB + AM + MC = AB + AM + BM = AM + AM = 2AM.
Khi giải các bài toán về vectơ, các em cần chú ý:
Ngoài Sách bài tập Toán 10 - Cánh Diều, các em có thể tham khảo thêm các tài liệu sau để nắm vững kiến thức về vectơ:
Hy vọng với lời giải chi tiết và hướng dẫn giải bài 35 trang 15 Sách bài tập Toán 10 - Cánh Diều trên đây, các em học sinh sẽ hiểu rõ hơn về vectơ và tự tin làm bài tập. Chúc các em học tập tốt!