Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và chính xác cho bài tập 30 trang 56 trong sách bài tập Toán 10 Cánh Diều. Chúng tôi hiểu rằng việc giải bài tập có thể gặp nhiều khó khăn, đặc biệt với những học sinh mới làm quen với chương trình Toán 10.
Với đội ngũ giáo viên giàu kinh nghiệm, chúng tôi đã biên soạn lời giải dễ hiểu, logic, giúp bạn nắm vững kiến thức và kỹ năng giải toán.
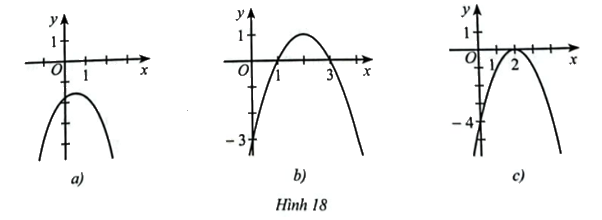
Dựa vào đồ thị hàm số bậc hai \(y = f\left( x \right)\) trong mỗi Hình 18a, 18b, 18c, hãy viết tập nghiệm các bất phương trình sau: \(f\left( x \right) > 0;f\left( x \right) < 0;f\left( x \right) \ge 0;f\left( x \right) \le 0\)
Đề bài
Dựa vào đồ thị hàm số bậc hai \(y = f\left( x \right)\) trong mỗi Hình 18a, 18b, 18c, hãy viết tập nghiệm các bất phương trình sau: \(f\left( x \right) > 0;f\left( x \right) < 0;f\left( x \right) \ge 0;f\left( x \right) \le 0\)
Phương pháp giải - Xem chi tiết
Phần đồ thị nằm dưới trục hoành tương ứng với \(f(x) < 0\)
Phần đồ thị nằm trên trục hoành tương ứng với \(f(x) > 0\)
Dựa vào parabol \(y = a{x^2} + bx + c\), ta tìm tập hợp những giá trị của \(x\) ứng với phần trên hoặc dưới trục hoành tùy dấu của tam thức bậc hai
Lời giải chi tiết
a) Quan sát đồ thị ở Hình 18a, ta có đồ thị hàm số \(y = f(x)\) nằm phía dưới trục hoành và không cắt trục hoành nên \(f\left( x \right) < 0\) với mọi \(x \in \mathbb{R}\). Do đó:
+ Tập nghiệm của BPT \(f\left( x \right) > 0\) là \(S = \emptyset \)
+ Tập nghiệm của BPT \(f\left( x \right) < 0\) là \(S = \mathbb{R}\)
+ Tập nghiệm của BPT \(f\left( x \right) \ge 0\) là \(S = \emptyset \)
+ Tập nghiệm của BPT \(f\left( x \right) \le 0\) là \(S = \mathbb{R}\)
b) Quan sát đồ thị ở Hình 18b, ta có:
Phần đồ thị nằm trên trục hoành ứng với \(1 < x < 3\)
Phần đồ thị nằm dưới trục hoành ứng với \(x < 1\) và \(x > 3\)
Đồ thị cắt trục hoành tại điểm có hoành độ \(x = 1\) và \(x = 3\)
Kết luận
+ Tập nghiệm của BPT \(f\left( x \right) > 0\) là \(S = \left( {1;3} \right)\)
+ Tập nghiệm của BPT \(f\left( x \right) < 0\) là \(S = \left( { - \infty ;1} \right) \cup \left( {3; + \infty } \right)\)
+ Tập nghiệm của BPT \(f\left( x \right) \ge 0\) là \(S = \left[ {1;3} \right]\)
+ Tập nghiệm của BPT \(f\left( x \right) \le 0\) là \(S = \left( { - \infty ;1} \right] \cup \left[ {3; + \infty } \right)\)
c) Quan sát đồ thị ở Hình 18c, ta có đồ thị hàm số \(y = f(x)\) nằm phía dưới trục hoành và cắt trục hoành tại A(2;0) nên \(f\left( x \right) \le 0\) với mọi \(x \in \mathbb{R}\).
+ Tập nghiệm của BPT \(f\left( x \right) > 0\) là \(S = \emptyset \)
+ Tập nghiệm của BPT \(f\left( x \right) < 0\) là \(S = \mathbb{R}{\rm{\backslash }}\{ 2\} \)
+ Tập nghiệm của BPT \(f\left( x \right) \ge 0\) là \(S = 2\)
+ Tập nghiệm của BPT \(f\left( x \right) \le 0\) là \(S = \mathbb{R}\)
Bài 30 trang 56 SBT Toán 10 Cánh Diều thuộc chương trình học về vectơ trong mặt phẳng. Bài tập này thường tập trung vào việc vận dụng các kiến thức về phép cộng, phép trừ vectơ, tích của một số với vectơ, và các tính chất của các phép toán này để giải quyết các bài toán hình học và đại số đơn giản.
Bài 30 thường bao gồm các dạng bài tập sau:
Để giải quyết bài 30 trang 56 SBT Toán 10 Cánh Diều một cách hiệu quả, bạn cần:
Ví dụ: Cho hai vectơ a = (2; -1) và b = (-3; 4). Tính 2a - b.
Giải:
2a = 2 * (2; -1) = (4; -2)
2a - b = (4; -2) - (-3; 4) = (4 - (-3); -2 - 4) = (7; -6)
Ngoài sách bài tập, bạn có thể tham khảo thêm các tài liệu sau để học tốt môn Toán 10:
Bài 30 trang 56 SBT Toán 10 Cánh Diều là một bài tập quan trọng giúp bạn củng cố kiến thức về vectơ. Hy vọng với hướng dẫn chi tiết và các ví dụ minh họa trên, bạn sẽ giải quyết bài tập này một cách dễ dàng và hiệu quả. Chúc bạn học tốt!