Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho bài tập 19 trang 39 sách bài tập Toán 10 - Cánh Diều. Bài viết này sẽ giúp bạn nắm vững kiến thức và kỹ năng giải toán, tự tin hơn trong quá trình học tập.
Chúng tôi hiểu rằng việc giải toán đôi khi có thể gặp khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn lời giải bài tập một cách cẩn thận, đảm bảo tính chính xác và dễ tiếp thu.
Biểu đồ đoạn thẳng ở Hình 4 cho biết kết quả thi Ngoại ngữ ở CLB của Dũng (đường nét liền) và Hoàng (đường nét đứt đậm) qua 9 lần kiểm tra
Đề bài
Biểu đồ đoạn thẳng ở Hình 4 cho biết kết quả thi Ngoại ngữ ở CLB của Dũng (đường nét liền) và Hoàng (đường nét đứt đậm) qua 9 lần kiểm tra
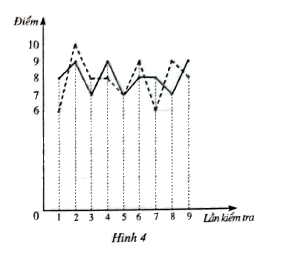
a) Viết mẫu số liệu thống kê kết quả thi ngoại ngữ của Dũng và Hoàng nhận được từ biểu đồ ở Hình 4
b) Tìm khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu đó
c) Tính phương sai và độ lệch chuẩn của hai mẫu số liệu đó. Cho biết kết quả thi của bạn nào ổn định hơn?
Phương pháp giải - Xem chi tiết
+ Liệt kê các giá trị trong biểu đồ và sắp xếp các số liệu theo thứ tự không giảm
+ Tìm khoảng biến thiên theo công thức\(R = {x_n} - {x_1}\) với số cao nhất và thấp nhất lần lượt \({x_n},{x_1}\)
+ Khoảng tứ phân vị: \(\Delta Q = {Q_3} - {Q_1}\)
Bước 1: Sắp xếp các số liệu theo thứ tự không giảm.
Bước 2: Tính cỡ mẫu \(n\), tìm tứ phân vị thứ hai \({Q_2}\)(chính là trung vị của mẫu).
Bước 3: Tìm tứ phân vị thứ nhất: là trung vị của nửa số liệu đã sắp xếp bên trái \({Q_2}\) (không bao gồm \({Q_2}\) nếu n lẻ)
Bước 4: Tìm tứ phân vị thứ ba: là trung vị của nửa số liệu đã sắp xếp bên phải \({Q_2}\) (không bao gồm \({Q_2}\) nếu n lẻ)
+ Tìm phương sai theo công thức \({S^2} = \frac{1}{n}\left( {{n_1}{x_1}^2 + {n_2}{x_2}^2 + ... + {n_k}{x_k}^2} \right) - {\overline x ^2}\) và độ lệch chuẩn \(S = \sqrt {{S^2}} \)
Lời giải chi tiết
a)
+ Mẫu số liệu kết quả thi của bạn Dũng là: 8; 9; 7; 9; 7; 8; 8; 7; 9.
+ Mẫu số liệu kết quả thi của bạn Hoàng là: 6; 10; 8; 8; 7; 9; 6; 9; 8.
b)
- Sắp xếp mẫu số liệu theo thứ tự tăng dần
Mẫu số liệu kết quả thi của bạn Dũng là: 7; 7; 7; 8; 8; 8; 9; 9; 9 (1)
Mẫu số liệu kết quả thi của bạn Hoàng là: 6; 6; 7; 8; 8; 8; 9; 9; 10 (2)
- Khoảng biến thiên:
+ Mẫu số liệu (1): Số cao nhất và thấp nhất lần lượt là 9 và 7 do đó khoảng biến thiên của dãy số liệu là: \(R = 9 - 7 = 2\)
+ Mẫu số liệu (2): Số cao nhất và thấp nhất lần lượt là 10 và 6 do đó khoảng biến thiên của dãy số liệu là: \(R = 10 - 6 = 4\)
- Mẫu số liệu (1):
+ Vì \(n = 9\) là số lẻ nên tứ phân vị thứ hai là: \({Q_2} = 8\) là tứ phân vị
+ Tứ phân vị thứ nhất là trung vị của 4 số đầu tiên của mẫu số liệu: \({Q_1} = \left( {7 + 7} \right):2 = 7\)
+ Tứ phân vị thứ ba là trung vị của 4 số cuối của mẫu số liệu: \({Q_3} = \left( {9 + 9} \right):2 = 9\)
+ Khoảng tứ phân vị: \(\Delta Q = {Q_3} - {Q_1} = 9 - 7 = 2\)
- Mẫu số liệu (2):
+ Vì \(n = 9\) là số lẻ nên tứ phân vị thứ hai là: \({Q_2} = 8\) là tứ phân vị
+ Tứ phân vị thứ nhất là trung vị của 4 số đầu tiên của mẫu số liệu: \({Q_1} = \left( {6 + 7} \right):2 = 6,5\)
+ Tứ phân vị thứ ba là trung vị của 4 số cuối của mẫu số liệu: \({Q_3} = \left( {9 + 9} \right):2 = 9\)
+ Khoảng tứ phân vị: \(\Delta Q = {Q_3} - {Q_1} = 9 - 6,5 = 2,5\)
c)
- Mẫu số liệu (1):
+ Số trung bình cộng: \(\overline x = \frac{{3.7 + 3.8 + 3.9}}{9} = 8\)
+ Phương sai: \({S^2} = \frac{1}{9}({3.7^2} + {3.8^2} + {3.9^2}) - {8^2} = \frac{2}{3}\)
+ Độ lệch chuẩn: \(S = \sqrt {{S^2}} = \sqrt {\frac{2}{3}} = \frac{{\sqrt 6 }}{3}\)
- Mẫu số liệu (2):
+ Số trung bình cộng: \(\overline x = \frac{{2.6 + 7 + 3.8 + 2.9 + 10}}{9} = \frac{{71}}{9}\)
+ Phương sai: \({S^2} = \frac{1}{9}({2.6^2} + {7^2} + {3.8^2} + {2.9^2} + {10^2}) - {\left( {\frac{{71}}{9}} \right)^2} = \frac{{134}}{{81}}\)
+ Độ lệch chuẩn: \(S = \sqrt {{S^2}} = \sqrt {\frac{{134}}{{81}}} = \frac{{\sqrt {134} }}{9}\)
Ta có: \(\frac{2}{3} < \frac{{134}}{{81}}\) nên kết quả thi của bạn Dũng ổn định hơn
Bài 19 trang 39 Sách bài tập Toán 10 - Cánh Diều tập trung vào việc ứng dụng phương pháp tọa độ để giải các bài toán hình học. Cụ thể, bài tập yêu cầu học sinh sử dụng hệ tọa độ để xác định vị trí của các điểm, đường thẳng, và tính toán các yếu tố hình học như khoảng cách, góc, diện tích.
Bài 19 bao gồm các dạng bài tập sau:
Để giải bài 19 trang 39 Sách bài tập Toán 10 - Cánh Diều một cách hiệu quả, bạn cần nắm vững các kiến thức sau:
Dưới đây là hướng dẫn giải chi tiết cho một số bài tập tiêu biểu trong bài 19:
Để giải bài tập này, bạn cần sử dụng tính chất của hình bình hành: hai đường chéo cắt nhau tại trung điểm của mỗi đường. Do đó, trung điểm của AC phải trùng với trung điểm của BD. Từ đó, bạn có thể thiết lập các phương trình để tìm tọa độ của điểm D.
Để viết phương trình đường thẳng đi qua hai điểm A và B, bạn có thể sử dụng công thức tính hệ số góc: m = (yB - yA) / (xB - xA). Sau đó, sử dụng phương trình đường thẳng dạng y = ax + b để tìm phương trình đường thẳng.
Để giải bài tập phương pháp tọa độ trong mặt phẳng một cách hiệu quả, bạn nên:
Giaitoan.edu.vn hy vọng rằng với hướng dẫn chi tiết này, bạn sẽ tự tin hơn trong việc giải bài 19 trang 39 Sách bài tập Toán 10 - Cánh Diều và đạt kết quả tốt trong môn Toán.
Để củng cố kiến thức và kỹ năng, bạn có thể luyện tập thêm các bài tập sau:
Chúc bạn học tập tốt!