Bài 30 trang 86 SBT Toán 10 Cánh Diều là một bài tập quan trọng trong chương trình học Toán 10. Bài tập này yêu cầu học sinh vận dụng kiến thức về vectơ, các phép toán vectơ và ứng dụng của vectơ trong hình học để giải quyết các bài toán cụ thể.
giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 30 trang 86 SBT Toán 10 Cánh Diều, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
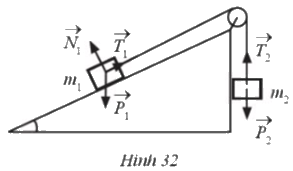
Trong mặt phẳng nghiêng không có ma sát, cho hệ vật m1, m2, hai vật nối với nhau bằng một sợi dây không dãn vắt qua ròng rọc (Hình 32). Giả sử bỏ qua khối lượng của dây và ma sát của ròng rọc
Đề bài
Trong mặt phẳng nghiêng không có ma sát, cho hệ vật m1, m2, hai vật nối với nhau bằng một sợi dây không dãn vắt qua ròng rọc (Hình 32). Giả sử bỏ qua khối lượng của dây và ma sát của ròng rọc
a) Tìm các cặp vectơ cùng phương trong các vectơ ở Hình 32
b) Những cặp vectơ cùng phương đó có cùng hướng không?
Phương pháp giải - Xem chi tiết
Bước 1: Tìm các cặp vectơ có giá song song hoặc trùng nhau
Bước 2: Dựa vào hướng các vectơ cùng phương xác định các vectơ cùng hướng
Lời giải chi tiết
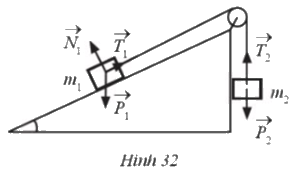
a) Các vectơ cùng phương là: \(\overrightarrow {{P_1}} \) và \(\overrightarrow {{P_2}} \), \(\overrightarrow {{P_1}} \) và \(\overrightarrow {{T_2}} \), \(\overrightarrow {{T_2}} \) và \(\overrightarrow {{P_2}} \)
b) Cặp vectơ \(\overrightarrow {{P_1}} \) và \(\overrightarrow {{P_2}} \) cùng hướng;
2 cặp vectơ \(\overrightarrow {{P_1}} \) và \(\overrightarrow {{T_2}} \), \(\overrightarrow {{T_2}} \) và \(\overrightarrow {{P_2}} \) ngược hướng
Bài 30 trang 86 SBT Toán 10 Cánh Diều thuộc chương trình học về vectơ trong không gian. Để giải quyết bài tập này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản như:
Bài tập thường yêu cầu học sinh chứng minh các đẳng thức vectơ, tìm tọa độ của vectơ, hoặc giải các bài toán hình học sử dụng vectơ.
Để cung cấp lời giải chi tiết, chúng ta cần xem xét từng câu hỏi cụ thể trong bài tập. Tuy nhiên, dưới đây là một ví dụ về cách tiếp cận giải một dạng bài tập thường gặp:
Vì M là trung điểm của BC, ta có: overrightarrow{BM} =overrightarrow{MC}. Do đó, overrightarrow{BC} = 2overrightarrow{BM}.
Ta có: overrightarrow{AM} =overrightarrow{AB} +overrightarrow{BM}. Thay overrightarrow{BM} = (1/2)overrightarrow{BC} vào, ta được:
overrightarrow{AM} =overrightarrow{AB} + (1/2)overrightarrow{BC}
Mà overrightarrow{BC} =overrightarrow{AC} -overrightarrow{AB}, nên:
overrightarrow{AM} =overrightarrow{AB} + (1/2)(overrightarrow{AC} -overrightarrow{AB}) =overrightarrow{AB} + (1/2)overrightarrow{AC} - (1/2)overrightarrow{AB} = (1/2)overrightarrow{AB} + (1/2)overrightarrow{AC} = (overrightarrow{AB} +overrightarrow{AC})/2
Vậy, overrightarrow{AM} = (overrightarrow{AB} +overrightarrow{AC})/2 (đpcm)
Bài 30 trang 86 SBT Toán 10 Cánh Diều là một bài tập quan trọng giúp học sinh củng cố kiến thức về vectơ và ứng dụng của vectơ trong hình học. Bằng cách nắm vững các khái niệm cơ bản, áp dụng các quy tắc cộng, trừ vectơ một cách linh hoạt và luyện tập thường xuyên, các em học sinh có thể tự tin giải quyết các bài tập về vectơ một cách hiệu quả.