Bài 54 trang 63 SBT Toán 10 Cánh Diều là một bài tập quan trọng trong chương trình học Toán 10. Bài tập này yêu cầu học sinh vận dụng kiến thức về vectơ, các phép toán vectơ và ứng dụng của vectơ trong hình học để giải quyết các bài toán cụ thể.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 54 trang 63 SBT Toán 10 Cánh Diều, giúp các em học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
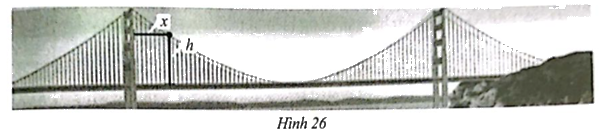
Quan sát chiếc Cổng Vàng (Golden Gate bridge) ở Hình 26
Đề bài
Quan sát chiếc Cổng Vàng (Golden Gate bridge) ở Hình 26. Độ cao \(h\) (feet) tính từ mặt cầu đến các điểm trên dây treo ở phần giữa hai trụ cầu được xác định bởi công thức \(h\left( x \right) = \frac{1}{{9000}}{x^2} - \frac{7}{{15}}x + 500\), trong đó \(x\) (feet) là khoảng cách từ trụ cầu bên trái đến điểm tương ứng trên dây treo
a) Xác định độ cao của trụ cầu so với mặt cầu theo đơn vị feet.
b) Xác định khoảng cách giữa hai trụ cầu theo đơn vị feet, biết rằng hai trụ cầu này có độ cao bằng nhau
Phương pháp giải - Xem chi tiết
Từ công thức ta tính toán các yêu cầu đề bài
Parabol \(y = a{x^2} + bx + c\): có trục đối xứng là đường thẳng \(x = - \frac{b}{{2a}}\)
Lời giải chi tiết
a) Độ cao của trụ cầu ứng với độ cao h tại \(x = 0\)
Tại \(x = 0\) thì \(h\left( 0 \right) = \frac{1}{{9000}}.0 - \frac{7}{{15}}.0 + 500 = 500\) (feet)
Vậy độ cao của trụ cầu so với mặt cầu là 500 feet.
b)
Dễ thấy hai đỉnh trụ cầu đối xứng với nhau qua trục đối xứng của parabol \(h(x)\).
Xác định trục đối xứng của parabol: \(x = \frac{{ - b}}{{2a}} = - \frac{{ - \frac{7}{{15}}}}{{2.\frac{1}{{9000}}}} = 2100\)
Khoảng cách giữa hai trụ cầu là \(2.2100 = 4200\) (feet)
Cách 2:
Do hai trụ cầu cao bằng nhau nên độ cao của trụ cầu bên phải cũng là 500 feet.
Khoảng cách giữa hai trụ cầu chính là hoành độ (khác 0) của trụ cầu bên phải.
Ta tìm \(x \ne 0\) sao cho \(h(x) = 500\)
\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}x \ne 0\\\frac{1}{{9000}}{x^2} - \frac{7}{{15}}x + 500 = 500\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ne 0\\\frac{1}{{9000}}{x^2} - \frac{7}{{15}}x = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ne 0\\\frac{1}{{9000}}x - \frac{7}{{15}} = 0\end{array} \right. \Leftrightarrow x = \frac{7}{{15}}:\frac{1}{{9000}} = 4200\end{array}\)
Vậy khoảng cách giữa hai trụ là 4200 feet.
Bài 54 trang 63 SBT Toán 10 Cánh Diều thuộc chương trình học về vectơ trong không gian. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các kiến thức cơ bản về vectơ, bao gồm:
Bài 54 thường yêu cầu học sinh thực hiện các nhiệm vụ sau:
Để giúp các em học sinh hiểu rõ hơn về cách giải bài tập này, chúng ta sẽ đi vào phân tích từng bước giải cụ thể. (Nội dung giải bài tập sẽ được trình bày chi tiết tại đây, bao gồm các bước giải, công thức sử dụng, và giải thích rõ ràng từng bước. Ví dụ: Giả sử bài tập yêu cầu tính độ dài của một vectơ, lời giải sẽ trình bày công thức tính độ dài vectơ, sau đó áp dụng công thức vào dữ liệu cụ thể của bài tập để tìm ra kết quả.)
Ví dụ 1: Cho hai điểm A(1; 2; 3) và B(4; 5; 6). Tìm vectơ AB và tính độ dài của vectơ AB.
Giải:
Ví dụ 2: Cho hai vectơ a = (1; -2; 3) và b = (2; 1; -1). Tính tích vô hướng của a và b.
Giải:
a.b = (1 * 2) + (-2 * 1) + (3 * -1) = 2 - 2 - 3 = -3
Để giải các bài tập về vectơ một cách hiệu quả, học sinh nên:
Để củng cố kiến thức và rèn luyện kỹ năng giải bài tập về vectơ, học sinh có thể tham khảo thêm các bài tập tương tự trong sách bài tập Toán 10 Cánh Diều và các tài liệu học tập khác. Ngoài ra, các em cũng có thể tìm kiếm các bài giảng trực tuyến hoặc tham gia các khóa học luyện thi để được hướng dẫn và giải đáp thắc mắc.
Bài 54 trang 63 SBT Toán 10 Cánh Diều là một bài tập quan trọng giúp học sinh hiểu sâu hơn về vectơ và ứng dụng của vectơ trong hình học. Bằng cách nắm vững kiến thức cơ bản, thực hành các phép toán vectơ và áp dụng các phương pháp giải hiệu quả, các em học sinh có thể tự tin giải quyết bài tập này và đạt kết quả tốt trong môn Toán.