Bài 64 trang 106 SBT Toán 10 - Cánh Diều là một bài tập quan trọng trong chương trình học Toán 10. Bài tập này yêu cầu học sinh vận dụng kiến thức về vectơ, các phép toán vectơ và ứng dụng của vectơ trong hình học để giải quyết các bài toán cụ thể.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 64 trang 106 SBT Toán 10 - Cánh Diều, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Cho hình vuông ABCD, M là trung điểm của BC. N là điểm nằm giữa hai điểm A và C. Đặt \(x = \frac{{AN}}{{AC}}\). Tìm x thỏa mãn \(AM \bot BN\)
Đề bài
Cho hình vuông ABCD, M là trung điểm của BC. N là điểm nằm giữa hai điểm A và C. Đặt \(x = \frac{{AN}}{{AC}}\). Tìm x thỏa mãn \(AM \bot BN\)
Phương pháp giải - Xem chi tiết
Bước 1: Tách và đưa các vectơ \(\overrightarrow {AM} ,\overrightarrow {BN} \) về vectơ chung gốc sao cho xuất hiện vectơ \(\overrightarrow {AN} ,\overrightarrow {AC} \)
Bước 2: Sử dụng tính chất \(AM \bot BN \Leftrightarrow \overrightarrow {AM} .\overrightarrow {BN} = 0\) để lập PT ẩn x
Bước 3: Giải PT ở bước 2 để tìm x và kết luận
Lời giải chi tiết
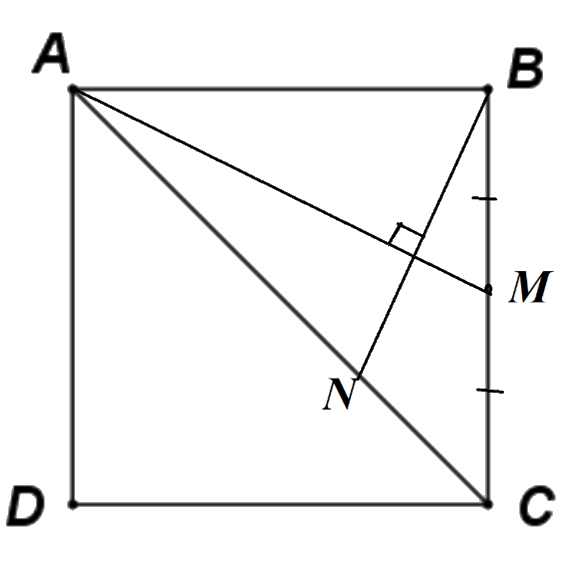
Do \(AM \bot BN\) nên \(\overrightarrow {AM} .\overrightarrow {BN} = 0\)
Ta có: \(x = \frac{{AN}}{{AC}} \Rightarrow AN = xAC \Rightarrow \overrightarrow {AN} = x\overrightarrow {AC} \)
\(\overrightarrow {AM} = \overrightarrow {BM} - \overrightarrow {BA} = \frac{1}{2}\overrightarrow {BC} - \overrightarrow {BA} \) ; \(\overrightarrow {BN} = \overrightarrow {AN} - \overrightarrow {AB} = x\overrightarrow {AC} - \overrightarrow {AB} \)
Khi đó \(\overrightarrow {AM} .\overrightarrow {BN} = 0\)\( \Leftrightarrow \left( {\frac{1}{2}\overrightarrow {BC} - \overrightarrow {BA} } \right).\left( {x\overrightarrow {AC} - \overrightarrow {AB} } \right) = 0\)
\( \Leftrightarrow \frac{x}{2}\overrightarrow {BC} .\overrightarrow {AC} - \frac{1}{2}\overrightarrow {BC} .\overrightarrow {AB} - x\overrightarrow {BA} .\overrightarrow {AC} + \overrightarrow {BA} .\overrightarrow {AB} = 0\)
\( \Leftrightarrow \frac{x}{2}.BC.\sqrt 2 BC.\cos {45^0} + x.AB.\sqrt 2 AB.\cos {45^0} - A{B^2} = 0\)
\( \Leftrightarrow \frac{x}{2} + x - 1 = 0 \Leftrightarrow x = \frac{2}{3}\)
Vậy với \(\frac{{AN}}{{AC}} = \frac{2}{3}\) thì \(AM \bot BN\)
Bài 64 trang 106 SBT Toán 10 - Cánh Diều thuộc chương trình học Toán 10, tập trung vào việc vận dụng kiến thức về vectơ để giải quyết các bài toán hình học. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản về vectơ, bao gồm:
Bài 64 trang 106 SBT Toán 10 - Cánh Diều thường yêu cầu học sinh thực hiện các thao tác sau:
(Ở đây sẽ là lời giải chi tiết của bài toán, bao gồm các bước giải, giải thích rõ ràng và hình vẽ minh họa nếu cần thiết. Ví dụ, nếu bài toán yêu cầu chứng minh một đẳng thức vectơ, lời giải sẽ trình bày các bước biến đổi để chứng minh đẳng thức đó. Nếu bài toán yêu cầu tính góc giữa hai vectơ, lời giải sẽ sử dụng công thức tích vô hướng để tính góc đó.)
Để giúp các em học sinh hiểu rõ hơn về phương pháp giải bài toán, chúng ta cùng xem xét một ví dụ minh họa:
Ví dụ: Cho tam giác ABC, với M là trung điểm của BC. Chứng minh rằng overrightarrow{AM} = (overrightarrow{AB} +overrightarrow{AC})/2.
Lời giải:
Để nắm vững kiến thức về vectơ và các ứng dụng của vectơ trong hình học, các em học sinh có thể tham khảo các tài liệu sau:
Bài 64 trang 106 SBT Toán 10 - Cánh Diều là một bài tập quan trọng giúp học sinh củng cố kiến thức về vectơ và rèn luyện kỹ năng giải toán. Hy vọng với lời giải chi tiết và phương pháp giải khoa học mà giaitoan.edu.vn cung cấp, các em học sinh sẽ tự tin hơn trong việc giải quyết bài toán này và đạt kết quả tốt trong môn Toán.