Giải bài 31 trang 15 Sách bài tập Toán 10 - Cánh Diều

Giải bài 31 trang 15 sách bài tập toán 10 - Cánh diều

Giải bài 31 trang 15 Sách bài tập Toán 10 - Cánh Diều

Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 31 trang 15 Sách bài tập Toán 10 - Cánh Diều. Bài viết này sẽ cung cấp cho bạn các bước giải bài tập một cách dễ hiểu, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập môn Toán.

Chúng tôi luôn cố gắng cung cấp những lời giải chính xác và đầy đủ nhất, đồng thời giải thích rõ ràng các khái niệm và công thức liên quan. Hãy cùng theo dõi bài viết này để hiểu rõ hơn về cách giải bài 31 trang 15 nhé!

Xác định các tập hợp sau

Đề bài

Xác định các tập hợp sau

a) \(\left[ { - 2;3} \right] \cap \left( {0;5} \right)\)

b) \(\left( { - 3;1} \right] \cap \left( {1; + \infty } \right)\)

c) \(\left( { - \infty ;0} \right) \cup \left( { - 2;2} \right]\)

d) \(\left( { - \infty ;0} \right) \cup \left[ {0; + \infty } \right)\)

e) \(\mathbb{R}\backslash \left[ {1; + \infty } \right)\)

g) \(\left[ {3;5} \right]\backslash \left( {4;6} \right)\)

Lời giải chi tiết

Giải bài 31 trang 15 sách bài tập toán 10 - Cánh diều 1

Vậy [– 2; 3] ∩ (0; 5) = (0; 3]

Giải bài 31 trang 15 sách bài tập toán 10 - Cánh diều 2

Vậy [– 3; 1] ∩ (1; +∞) = ∅

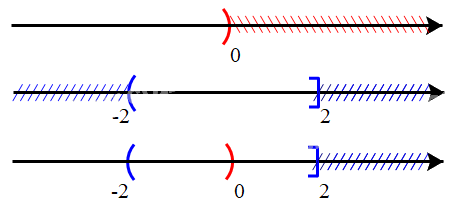
Giải bài 31 trang 15 sách bài tập toán 10 - Cánh diều 3

Vậy (– ∞; 0) ∪ (– 2; 2] = (– ∞; 2].

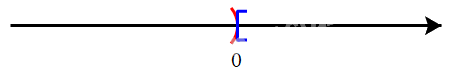
Giải bài 31 trang 15 sách bài tập toán 10 - Cánh diều 4

Vậy (– ∞; 0) ∪ [0; +∞) = (– ∞; +∞) = ℝ

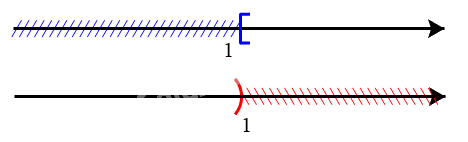
Giải bài 31 trang 15 sách bài tập toán 10 - Cánh diều 5

Vậy ℝ \ [1; +∞) = (–∞; 1)

Giải bài 31 trang 15 sách bài tập toán 10 - Cánh diều 6

Vậy [3; 5] \ (4; 6) = [3; 4]

Xây dựng nền tảng Toán THPT vững vàng từ hôm nay! Đừng bỏ lỡ Giải bài 31 trang 15 sách bài tập toán 10 - Cánh diều đặc sắc thuộc chuyên mục bài tập toán 10 trên nền tảng tài liệu toán. Với bộ bài tập toán thpt được biên soạn chuyên sâu, bám sát chương trình Toán lớp 10, đây chính là "kim chỉ nam" giúp các em tối ưu hóa ôn luyện, củng cố kiến thức cốt lõi và chuẩn bị hành trang vững chắc cho tương lai. Phương pháp học trực quan, logic sẽ mang lại hiệu quả vượt trội trên lộ trình chinh phục đại học!

Giải bài 31 trang 15 Sách bài tập Toán 10 - Cánh Diều: Phương pháp tiếp cận và lời giải chi tiết

Bài 31 trang 15 Sách bài tập Toán 10 - Cánh Diều thuộc chương trình học về hàm số bậc hai. Để giải bài tập này một cách hiệu quả, chúng ta cần nắm vững các kiến thức cơ bản về:

Định nghĩa hàm số bậc hai
Các dạng biểu diễn của hàm số bậc hai (dạng tổng quát, dạng chuẩn)
Đồ thị hàm số bậc hai (đỉnh, trục đối xứng, giao điểm với các trục tọa độ)
Các tính chất của hàm số bậc hai (tính đơn điệu, giá trị lớn nhất, giá trị nhỏ nhất)

Nội dung bài 31: Bài tập yêu cầu xác định các hệ số a, b, c của hàm số bậc hai, tìm đỉnh của parabol, vẽ đồ thị hàm số và khảo sát sự biến thiên của hàm số.

Lời giải chi tiết bài 31 trang 15 Sách bài tập Toán 10 - Cánh Diều

Để giải bài 31, chúng ta sẽ tiến hành theo các bước sau:

Xác định các hệ số a, b, c: Dựa vào phương trình hàm số đã cho, ta xác định các hệ số a, b, c. Ví dụ, nếu hàm số có dạng y = ax² + bx + c, thì a là hệ số của x², b là hệ số của x, và c là hệ số tự do.
Tìm đỉnh của parabol: Đỉnh của parabol có tọa độ (x₀, y₀), trong đó x₀ = -b/(2a) và y₀ = f(x₀).
Vẽ đồ thị hàm số: Để vẽ đồ thị hàm số, ta cần xác định một số điểm thuộc đồ thị, bao gồm đỉnh, giao điểm với các trục tọa độ và một vài điểm khác.
Khảo sát sự biến thiên của hàm số: Dựa vào dấu của hệ số a, ta có thể xác định chiều của parabol (lõm lên hay lõm xuống). Ngoài ra, ta cũng cần xét dấu của biểu thức f(x) để xác định khoảng mà hàm số dương, âm hoặc bằng 0.

Ví dụ minh họa:

Giả sử hàm số được cho là y = 2x² - 8x + 6.

Xác định các hệ số: a = 2, b = -8, c = 6.
Tìm đỉnh: x₀ = -(-8)/(2*2) = 2; y₀ = 2*(2)² - 8*2 + 6 = -2. Vậy đỉnh của parabol là (2, -2).
Vẽ đồ thị: Xác định thêm một vài điểm khác, ví dụ: x = 0 => y = 6; x = 1 => y = 0; x = 3 => y = 0.
Khảo sát: Vì a = 2 > 0, parabol có chiều lõm lên. Hàm số dương khi x < 1 hoặc x > 3, âm khi 1 < x < 3.

Lưu ý:

Khi giải bài tập về hàm số bậc hai, cần chú ý đến các điều kiện xác định của hàm số.
Sử dụng máy tính bỏ túi hoặc phần mềm vẽ đồ thị để kiểm tra lại kết quả.
Luyện tập thường xuyên để nắm vững các kiến thức và kỹ năng giải bài tập.

Các bài tập tương tự:

Để củng cố kiến thức, bạn có thể luyện tập thêm các bài tập tương tự trong sách bài tập Toán 10 - Cánh Diều hoặc các nguồn tài liệu học tập khác. Việc giải nhiều bài tập sẽ giúp bạn hiểu rõ hơn về các khái niệm và công thức, đồng thời rèn luyện kỹ năng giải bài tập một cách nhanh chóng và chính xác.

Giaitoan.edu.vn hy vọng rằng bài viết này đã cung cấp cho bạn những thông tin hữu ích và giúp bạn giải bài 31 trang 15 Sách bài tập Toán 10 - Cánh Diều một cách dễ dàng. Chúc bạn học tập tốt!