Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 10. Bài viết này sẽ hướng dẫn bạn cách giải bài 44 trang 61 SBT Toán 10 - Cánh Diều một cách nhanh chóng và hiệu quả.
Chúng tôi luôn cố gắng cung cấp nội dung chất lượng cao, giúp bạn học Toán 10 một cách tốt nhất. Hãy cùng bắt đầu nhé!
Người ta muốn thiết kế một vườn hoa hình chữ nhật nội tiếp trong một miếng đất hình tròn có đường kính bằng 50 m (Hình 23).
Đề bài
Người ta muốn thiết kế một vườn hoa hình chữ nhật nội tiếp trong một miếng đất hình tròn có đường kính bằng 50 m (Hình 23). Xác định kích thước vườn hoa hình chữ nhật để tổng quãng đường đi xung quanh vườn hoa đó là 140 m.
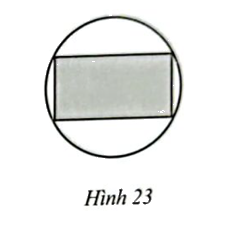
Phương pháp giải - Xem chi tiết
Đặt độ dài 1 cạnh của hình chữ nhật là \(x\)(m) (\(0 < x < 50\)).
Biểu diễn cạnh còn lại và chu vi của hình chữ nhật theo x.
Lời giải chi tiết
Đặt độ dài một cạnh của hình chữ nhật là \(x\)(m) (\(0 < x < 50\)).
Độ dài đường chéo hình chữ nhật = Đường kính đường tròn = 50m.
Độ dài cạnh còn lại của hình chữ nhật đó là \(\sqrt {{{50}^2} - {x^2}} = \sqrt {2500 - {x^2}} \) (m)
Khi đó, tổng quãng đường đi xung quanh vườn hoa bằng chu vi hình chữ nhật là: \(2\left( {\sqrt {2500 - {x^2}} + x} \right) = 140\) (m)
Ta có phương trình: \(2\left( {\sqrt {2500 - {x^2}} + x} \right) = 140 \Leftrightarrow \sqrt {2500 - {x^2}} + x = 70 \Rightarrow \sqrt {2500 - {x^2}} = 70 - x\)
\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}x > 0\\70 - x \ge 0\\2500 - {x^2} = {\left( {70 - x} \right)^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}0 < x \le 70\\2500 - {x^2} = {x^2} - 140x + {70^2}\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}0 < x \le 70\\2{x^2} - 140x + 2400 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}0 < x \le 70\\\left[ \begin{array}{l}x = 30\\x = 40\;\end{array} \right.\quad \end{array} \right.\end{array}\)
Nếu \(x = 40\) thì độ dài cạnh còn lại là 30 (m) và ngược lại.
Vậy kích thước vườn hoa là 30 x 40 (m)
Bài 44 trang 61 SBT Toán 10 - Cánh Diều thuộc chương trình học Toán 10, tập trung vào việc vận dụng các kiến thức về vectơ để giải quyết các bài toán hình học. Bài tập này yêu cầu học sinh phải nắm vững các khái niệm như vectơ, phép cộng, phép trừ vectơ, tích của một số với vectơ, và các tính chất liên quan.
Bài 44 thường bao gồm các dạng bài tập sau:
Để giải quyết bài 44 trang 61 SBT Toán 10 - Cánh Diều một cách hiệu quả, bạn có thể áp dụng các phương pháp sau:
(Phần này sẽ trình bày lời giải chi tiết cho từng câu hỏi của bài 44. Do bài tập có thể thay đổi theo thời gian, nên phần này sẽ được cập nhật thường xuyên để đảm bảo tính chính xác.)
Ví dụ, xét câu a của bài 44:
Cho A(1; 2), B(3; 4). Tìm tọa độ của vectơ AB.
Lời giải:
Vectơ AB có tọa độ là (3 - 1; 4 - 2) = (2; 2).
Để củng cố kiến thức và kỹ năng giải bài tập về vectơ, bạn có thể tham khảo các bài tập tương tự sau:
Bài 44 trang 61 SBT Toán 10 - Cánh Diều là một bài tập quan trọng giúp bạn rèn luyện kỹ năng giải quyết các bài toán hình học bằng vectơ. Hy vọng rằng, với những hướng dẫn chi tiết và phương pháp giải hiệu quả mà chúng tôi đã cung cấp, bạn sẽ tự tin hơn trong việc học Toán 10.
| Công thức | Mô tả |
|---|---|
| AB = B - A | Vectơ AB bằng hiệu tọa độ của điểm B và điểm A |
| k.AB = (kx; ky) | Tích của một số k với vectơ AB |
| M là trung điểm của AB | Tọa độ của M là ((xA + xB)/2; (yA + yB)/2) |