Bài 20 trang 80 SBT Toán 10 Cánh Diều là một bài tập quan trọng trong chương trình học Toán 10, tập trung vào việc rèn luyện kỹ năng về vectơ và các phép toán vectơ. Bài tập này đòi hỏi học sinh phải nắm vững kiến thức lý thuyết và áp dụng linh hoạt vào giải quyết các bài toán cụ thể.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 20 trang 80 SBT Toán 10 Cánh Diều, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Quan sát cây cầu dây văng minh họa ở Hình 25
Đề bài
Quan sát cây cầu dây văng minh họa ở Hình 25
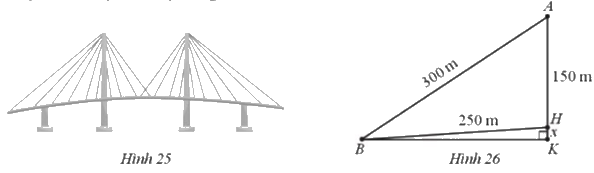
Tại trụ cao nhất, khoảng cách từ đỉnh trụ (vị trí A) tới chân trụ trên mặt cầu (vị trí H) là 150 m, độ dài dây văng dài nhất nối từ đỉnh trụ xuống mặt cầu (vị trí B) là 300 m, khoảng cách từ chân dây văng dài nhất tới chân trụ trên mặt cầu là 250 m (Hình 26). Tính độ dốc của cầu qua trụ nói trên (làm tròn kết quả đến hàng phần mười theo đơn vị độ).
Phương pháp giải - Xem chi tiết
Độ dốc của cầu là góc nghiêng HBK
Bước 1: Sử dụng định lí cosin để tính số đo góc AHB của ∆ABH
Bước 2: Sử dụng tính chất góc ngoài của tam giác (xét ∆HBK) để tính góc HBK rồi kết luận
Lời giải chi tiết
Áp dụng định lí cosin cho ∆ABH ta có: \(A{B^2} = B{H^2} + A{H^2} - 2.BH.AH.\cos \widehat {AHB}\)
\( \Rightarrow \cos \widehat {AHB} = \frac{{B{H^2} + A{H^2} - A{B^2}}}{{2.BH.AH}} = \frac{{{{250}^2} + {{150}^2} - {{300}^2}}}{{2.250.150}} = - \frac{1}{{15}}\)\( \Rightarrow \widehat {AHB} \approx 93,{8^0}\)
Xét ∆HBK có \(\widehat {AHB}\) là góc ngoài của tam giác HBK
\( \Rightarrow \widehat {AHB} = \widehat {HBK} + \widehat {HKB} \Rightarrow \widehat {HBK} = \widehat {AHB} - \widehat {HKB} = 93,{8^0} - {90^0} = 3,{8^0}\)
Vậy độ dốc của cầu qua trụ là 3,80
Bài 20 trang 80 SBT Toán 10 Cánh Diều thuộc chương trình học về vectơ trong không gian. Để giải quyết bài toán này, học sinh cần nắm vững các kiến thức cơ bản về vectơ, bao gồm:
Bài 20 thường bao gồm các dạng bài tập sau:
Để giúp các em học sinh hiểu rõ hơn về cách giải bài 20 trang 80 SBT Toán 10 Cánh Diều, chúng ta sẽ đi vào giải chi tiết từng câu hỏi. (Lưu ý: Vì nội dung bài tập cụ thể không được cung cấp, phần này sẽ trình bày phương pháp giải tổng quát và ví dụ minh họa.)
Bài toán: Cho tam giác ABC, với A(1;2), B(3;4), C(5;0). Tính độ dài cạnh AB và góc BAC.
Lời giải:
Để học tốt môn Toán 10, các em có thể tham khảo các tài liệu sau:
Bài 20 trang 80 SBT Toán 10 Cánh Diều là một bài tập quan trọng giúp các em học sinh củng cố kiến thức về vectơ và các phép toán vectơ. Hy vọng với hướng dẫn chi tiết và phương pháp giải trên, các em sẽ tự tin giải quyết bài tập này một cách hiệu quả. Chúc các em học tốt!