Bài 39 trang 92 SBT Toán 10 Cánh Diều là một bài tập quan trọng trong chương trình học Toán 10. Bài tập này yêu cầu học sinh vận dụng kiến thức về vectơ, các phép toán vectơ và ứng dụng của vectơ trong hình học để giải quyết các bài toán cụ thể.
giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 39 trang 92 SBT Toán 10 - Cánh Diều, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Cho tam giác đều ABC cạnh a. Tính:
Đề bài
Cho tam giác đều ABC cạnh a. Tính:
a) \(\left| {\overrightarrow {AB} + \overrightarrow {BC} } \right|\)
b) \(\left| {\overrightarrow {AB} - \overrightarrow {AC} } \right|\)
c) \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right|\)
Phương pháp giải - Xem chi tiết
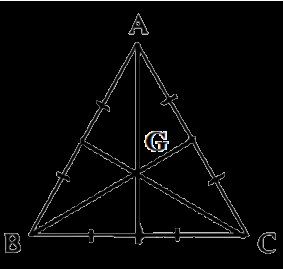
Bước 1: Lấy G là trọng tâm tam giác ABC
Bước 2: Sử dụng quy tắc cộng, quy tắc trừ, quy tắc 3 điểm (lấy G là điểm trung gian) để biến đổi và tính độ dài các vectơ tương ứng
Lời giải chi tiết
Gọi G là trọng tâm tam giác ABC
Khi đó \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \), \(GA = GB = GC = \frac{{a\sqrt 3 }}{3}\)
a)Ta có: \(\left| {\overrightarrow {AB} + \overrightarrow {BC} } \right| = \left| {\overrightarrow {AC} } \right| = AC = a\)
b) Ta có: \(\left| {\overrightarrow {AB} - \overrightarrow {AC} } \right| = \left| {\overrightarrow {CB} } \right| = BC = a\)
c) Ta có: \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = \left| {\left( {\overrightarrow {GB} - \overrightarrow {GA} } \right) + \left( {\overrightarrow {GC} - \overrightarrow {GA} } \right)} \right| = \left| {\left( {\overrightarrow {GB} + \overrightarrow {GC} } \right) - 2\overrightarrow {GA} } \right|\) (1)
Lại có: \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \Leftrightarrow \overrightarrow {GB} + \overrightarrow {GC} = - \overrightarrow {GA} \) (2)
Từ (1) và (2) suy ra \(\left| {\overrightarrow {AB} + \overrightarrow {AC} } \right| = \left| { - \overrightarrow {GA} - 2\overrightarrow {GA} } \right| = \left| { - 3\overrightarrow {GA} } \right| = 3\left| {\overrightarrow {GA} } \right| = 3GA = 3.\frac{{a\sqrt 3 }}{3} = a\sqrt 3 \)
Bài 39 trang 92 SBT Toán 10 Cánh Diều thuộc chương trình học về vectơ trong không gian. Để giải bài tập này, học sinh cần nắm vững các kiến thức cơ bản về vectơ, bao gồm:
Bài 39 trang 92 SBT Toán 10 Cánh Diều thường yêu cầu học sinh thực hiện các nhiệm vụ sau:
Để giúp các em học sinh hiểu rõ hơn về cách giải bài tập này, chúng ta sẽ đi vào phân tích từng bước cụ thể. (Nội dung lời giải chi tiết sẽ được trình bày ở đây, bao gồm các bước giải, công thức sử dụng, và giải thích rõ ràng từng bước. Ví dụ:)
Ví dụ: Giả sử bài tập yêu cầu chứng minh rằng tứ giác ABCD là hình bình hành. Ta có thể sử dụng vectơ để chứng minh điều này bằng cách chứng minh rằng AB = DC và AD = BC.
Để chứng minh AB = DC, ta cần chứng minh rằng AB và DC cùng hướng và có độ dài bằng nhau. Tương tự, để chứng minh AD = BC, ta cần chứng minh rằng AD và BC cùng hướng và có độ dài bằng nhau.
Để giải các bài tập về vectơ một cách hiệu quả, các em học sinh có thể tham khảo một số mẹo sau:
Vectơ không chỉ là một khái niệm trừu tượng trong toán học mà còn có nhiều ứng dụng thực tế trong các lĩnh vực khác nhau, như:
Bài 39 trang 92 SBT Toán 10 Cánh Diều là một bài tập quan trọng giúp các em học sinh củng cố kiến thức về vectơ và ứng dụng của vectơ trong hình học. Hy vọng rằng với lời giải chi tiết và các mẹo giải bài tập hiệu quả mà giaitoan.edu.vn đã cung cấp, các em học sinh sẽ tự tin hơn trong việc giải quyết các bài tập tương tự.
Hãy luyện tập thường xuyên để nắm vững kiến thức và đạt kết quả tốt nhất trong môn Toán 10!