Bài 23 trang 52 SBT Toán 10 Cánh Diều là một bài tập quan trọng trong chương trình học Toán 10. Bài tập này yêu cầu học sinh vận dụng kiến thức về vectơ, các phép toán vectơ và ứng dụng của vectơ trong hình học để giải quyết các bài toán cụ thể.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 23 trang 52 SBT Toán 10 Cánh Diều, giúp các em học sinh nắm vững kiến thức và rèn luyện kỹ năng giải toán.
Lập bảng xét dấu mỗi tam thức bậc hai sau:
Đề bài
Lập bảng xét dấu mỗi tam thức bậc hai sau:
a) \(f\left( x \right) = 3{x^2} - 7x + 4\)
b) \(f\left( x \right) = 25{x^2} + 10x + 1\)
c) \(f\left( x \right) = 3{x^2} - 2x + 8\)
d) \(f\left( x \right) = - 2{x^2} + x + 3\)
e) \(f\left( x \right) = - 3{x^2} + 6x - 3\)
g) \(f\left( x \right) = - 5{x^2} + 2x - 4\)
Phương pháp giải - Xem chi tiết
Cho tam thức bậc hai \(f\left( x \right) = a{x^2} + bx + c\left( {a \ne 0} \right),\Delta = {b^2} - 4ac\)
+ Nếu \(\Delta < 0\) thì \(f\left( x \right)\) cùng dấu với hệ số \(a\) với mọi \(x \in \mathbb{R}\)
+ Nếu \(\Delta = 0\) thì \(f\left( x \right)\) cùng dấu với hệ số \(a\) với mọi \(x \in \mathbb{R}\backslash \left\{ {\frac{{ - b}}{{2a}}} \right\}\)
+ Nếu \(\Delta > 0\) thì \(f\left( x \right)\) có hai nghiệm \({x_1},{x_2}\left( {{x_1} < {x_2}} \right)\). Khi đó:

Lời giải chi tiết
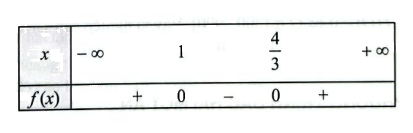
a) \(f\left( x \right) = 3{x^2} - 7x + 4\) có hai nghiệm \({x_1} = 1;{x_2} = \frac{4}{3}\) và có hệ số \(a = 3 > 0\)
Ta có bảng xét dấu của \(f\left( x \right)\) như sau:
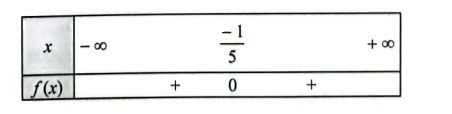
b) \(f\left( x \right) = 25{x^2} + 10x + 1\) có nghiệm kép \({x_0} = \frac{{ - 1}}{5}\) và có hệ số \(a = 25 > 0\)
Ta có bảng xét dấu của \(f\left( x \right)\) như sau:
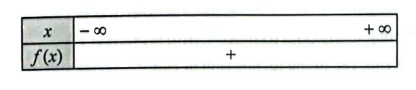
c) \(f\left( x \right) = 3{x^2} - 2x + 8\) vô nghiệm và có hệ số \(a = 3 > 0\)
Ta có bảng xét dấu của \(f\left( x \right)\) như sau:
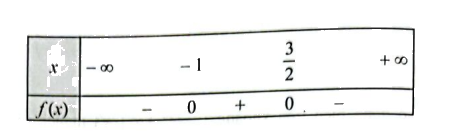
d) \(f\left( x \right) = - 2{x^2} + x + 3\) có hai nghiệm \({x_1} = - 1;{x_2} = \frac{3}{2}\) và có hệ số \(a = - 2 < 0\)
Ta có bảng xét dấu của \(f\left( x \right)\) như sau:
e) \(f\left( x \right) = - 3{x^2} + 6x - 3\) có nghiệm kép \({x_0} = 1\) và có hệ số \(a = - 3 < 0\)
Ta có bảng xét dấu của \(f\left( x \right)\) như sau:

g) \(f\left( x \right) = - 5{x^2} + 2x - 4\) vô nghiệm và có hệ số \(a = - 5 < 0\)
Ta có bảng xét dấu của \(f\left( x \right)\) như sau:

Bài 23 trang 52 SBT Toán 10 Cánh Diều thuộc chương trình học về vectơ trong không gian. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các khái niệm cơ bản về vectơ, bao gồm:
Bài 23 trang 52 SBT Toán 10 Cánh Diều thường bao gồm các dạng bài tập sau:
Để giúp các em học sinh hiểu rõ hơn về cách giải bài tập này, chúng ta sẽ đi vào giải chi tiết từng phần của bài tập. (Ở đây sẽ là nội dung giải chi tiết bài tập, bao gồm các bước giải, giải thích và kết luận. Nội dung này sẽ rất dài và chi tiết, bao gồm các ví dụ minh họa và các lưu ý quan trọng.)
Ví dụ 1: Cho hai điểm A(1; 2; 3) và B(4; 5; 6). Tìm tọa độ của vectơ AB.
Giải: Vectơ AB có tọa độ là (4-1; 5-2; 6-3) = (3; 3; 3).
Ví dụ 2: Cho vectơ a = (1; 2; 3) và vectơ b = (4; 5; 6). Tính tổng của hai vectơ a và b.
Giải: Vectơ a + b có tọa độ là (1+4; 2+5; 3+6) = (5; 7; 9).
Bài 23 trang 52 SBT Toán 10 Cánh Diều là một bài tập quan trọng giúp học sinh củng cố kiến thức về vectơ và rèn luyện kỹ năng giải toán. Hy vọng với hướng dẫn chi tiết và phương pháp giải hiệu quả trên đây, các em học sinh sẽ tự tin giải quyết bài tập này một cách thành công.