Chào mừng các em học sinh đến với lời giải chi tiết bài 29 trang 85 SBT Toán 10 - Cánh Diều tại giaitoan.edu.vn. Bài viết này sẽ cung cấp cho các em phương pháp giải bài tập hiệu quả, giúp các em hiểu rõ kiến thức và tự tin hơn trong quá trình học tập.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, giúp các em chinh phục môn Toán một cách dễ dàng.
Cho tam giác ABC. Gọi M, N, P lần lượt là trung điểm của BC, CA, AB. Chứng minh rằng:
Đề bài
Cho tam giác ABC. Gọi M, N, P lần lượt là trung điểm của BC, CA, AB. Chứng minh rằng:
a) \(\overrightarrow {MN} = \overrightarrow {PA} \)
b) \(\overrightarrow {MP} = \overrightarrow {CN} \)
Phương pháp giải - Xem chi tiết
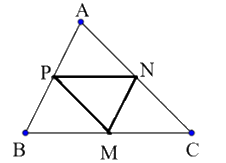
Bước 1: Chứng minh MNAP là hình bình hành rồi suy ra \(\overrightarrow {MN} = \overrightarrow {PA} \)
Bước 2: Chứng minh MPNC là hình bình hành rồi suy ra \(\overrightarrow {MP} = \overrightarrow {CN} \)
Lời giải chi tiết
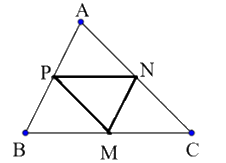
a) Theo giả thiết, MN là đường trung bình của tam giác ABC \( \Rightarrow MN//AB,MN = \frac{1}{2}AB\)
mà P là trung điểm AB nên \(MN//AP,MN = AP\)
Do đó MNAP là hình bình hành \( \Rightarrow \)\(\overrightarrow {MN} = \overrightarrow {PA} \)
a) Theo giả thiết, MP là đường trung bình của tam giác ABC \( \Rightarrow MP//AC,MP = \frac{1}{2}AC\)
mà N là trung điểm AC nên \(MP//AN,MP = AN\)
Do đó MPNC là hình bình hành \( \Rightarrow \)\(\overrightarrow {MP} = \overrightarrow {CN} \)
Bài 29 trang 85 SBT Toán 10 - Cánh Diều thuộc chương trình học Toán 10, tập trung vào việc vận dụng các kiến thức về vectơ để giải quyết các bài toán hình học. Bài tập này yêu cầu học sinh phải nắm vững các khái niệm như vectơ, phép cộng, phép trừ vectơ, tích của một số với vectơ, và các tính chất liên quan.
Bài 29 bao gồm một số câu hỏi và bài tập nhỏ, yêu cầu học sinh:
Đề bài: Cho hình bình hành ABCD. Tìm vectơ bằng vectơ AB.
Lời giải: Trong hình bình hành ABCD, ta có AB = DC và AD = BC. Do đó, vectơ bằng vectơ AB là vectơ DC.
Đề bài: Cho tam giác ABC. Tìm vectơ bằng vectơ CA.
Lời giải: Vectơ bằng vectơ CA là vectơ AC (vì CA = -AC).
Đề bài: Cho bốn điểm A, B, C, D. Chứng minh rằng AB + BC = AC.
Lời giải: Theo quy tắc cộng vectơ, nếu B nằm giữa A và C thì AB + BC = AC. Điều này thể hiện mối quan hệ giữa các vectơ trong một đường thẳng.
Để giải các bài tập về vectơ một cách hiệu quả, các em cần:
Ví dụ 1: Cho tam giác ABC, M là trung điểm của BC. Chứng minh rằng 2MA = AB + AC.
Lời giải:
Ta có: MA = MB + BA và MA = MC + CA.
Cộng hai đẳng thức trên, ta được: 2MA = MB + BA + MC + CA.
Vì M là trung điểm của BC nên MB = MC. Do đó: 2MA = 2MB + BA + CA.
Mà MB = 1/2 BC nên 2MA = BC + BA + CA = BC + (BA + CA) = BC + CB = 0 (sai).
Cách giải đúng:
MA = MB + BA
MA = MC + CA
2MA = MB + BA + MC + CA
2MA = MB + MC + BA + CA
2MA = BC + BA + CA
2MA = BC + (BA + CA)
2MA = BC + CB = 0 (vẫn sai)
Sử dụng quy tắc hình bình hành: AB + AC = 2AM => AM = (AB + AC)/2 => 2AM = AB + AC
Để củng cố kiến thức, các em có thể tự giải các bài tập sau:
Hy vọng với lời giải chi tiết và phương pháp giải bài tập vectơ được trình bày trên đây, các em sẽ tự tin hơn trong việc học tập môn Toán 10. Chúc các em học tốt!