Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong sách bài tập Toán 10 Cánh Diều. Bài viết này sẽ hướng dẫn bạn từng bước giải bài 43 trang 61, giúp bạn hiểu rõ bản chất của bài toán và áp dụng kiến thức vào các bài tập tương tự.
Chúng tôi luôn cố gắng cung cấp nội dung chất lượng cao, chính xác và cập nhật nhất để hỗ trợ bạn trong quá trình học tập môn Toán.
Một người đi bộ xuất phát từ B trên một bờ sông (coi là đường thẳng) với vận tốc 6 km/h để gặp một người chèo thuyền xuất phát cùng lúc từ vị trí A với vận tốc 3 km/h.
Đề bài
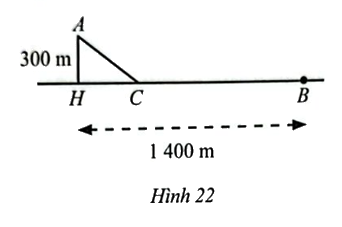
Một người đi bộ xuất phát từ B trên một bờ sông (coi là đường thẳng) với vận tốc 6 km/h để gặp một người chèo thuyền xuất phát cùng lúc từ vị trí A với vận tốc 3 km/h. Nếu người chèo thuyền di chuyển theo đường vuông góc với bờ thì phải đi một khoảng cách AH = 300 m và người đi bộ tại địa điểm cách B một khoảng BH = 1 400 m. Tuy nhiên, nếu di chuyển theo cách đó thì hai người không tới cùng lúc. Để hai người đến cùng lúc thì mỗi người cùng di chuyển về vị trí C (Hình 22).
a) Tính khoảng các CB
b) Tính thời gian từ khi hai người xuất phát cho đến khi gặp nhau cùng lúc
Phương pháp giải - Xem chi tiết
Gọi \(CH = x\) (m). Biểu diễn AC và BC qua x. Giải phương trình \(\frac{{AC}}{{3.000}} = \frac{{BC}}{{6.000}}\) tìm ra CH
Lời giải chi tiết
a) Đặt \(CH = x\) (m) (\(x > 0\)). Ta có: \(AC = \sqrt {A{H^2} + C{H^2}} = \sqrt {{{300}^2} + {x^2}} ,BC = 1\;400 - CH = 1\;400 - x\)
Đổi 6 km/h = 6000 m/h; 3 km/h = 3000 m/h;
Thời gian đi đến lúc gặp nhau của người đi bộ là: \(\frac{{BC}}{{6000}} = \frac{{1400 - x}}{{6000}}\)
Thời gian đi đến lúc gặp nhau của người chèo thuyền là: \(\frac{{AC}}{{3000}} = \frac{{\sqrt {{{300}^2} + {x^2}} }}{{3000}}\)
Vì hai người gặp nhau cùng lúc tại C nên ta có: \(\frac{{\sqrt {{{300}^2} + {x^2}} }}{{3000}} = \frac{{1400 - x}}{{6000}} \Leftrightarrow 2\sqrt {{{300}^2} + {x^2}} = 1400 - x\) (với \(x > 0\))
\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}x > 0\\1400 - x \ge 0\\4\left( {{{300}^2} + {x^2}} \right) = {\left( {1400 - x} \right)^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}0 < x \le 1400\\4{x^2} + 360000 = {x^2} - 2800x + {1400^2}\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}0 < x \le 1400\\3{x^2} + 2800x - 1600000 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}0 < x \le 1400\\\left[ \begin{array}{l}x = - \frac{{4000}}{3}\;(L)\\x = 400\;\end{array} \right.\quad \end{array} \right. \Leftrightarrow x = 400\;\end{array}\)
Vậy khoảng cách \(BC = 1400 - 400 = 1000\) (m)
b) Thời gian từ khi hai người xuất phát cho đến khi gặp nhau là thời gian người đi bộ bắt đầu di chuyển cho đến khi gặp người chèo thuyền tại C là:
\(\frac{{BC}}{{6000}} = \frac{{1000}}{{6000}} = \frac{1}{6}\) (giờ) = 10 phút.
Bài 43 trang 61 SBT Toán 10 Cánh Diều thuộc chương trình học về vectơ trong mặt phẳng. Bài toán này thường yêu cầu học sinh vận dụng các kiến thức về phép cộng, trừ vectơ, tích của một số với vectơ, và các tính chất của chúng để giải quyết các bài toán liên quan đến hình học phẳng.
Bài 43 thường bao gồm các dạng bài tập sau:
Để giải bài 43 trang 61 SBT Toán 10 Cánh Diều một cách hiệu quả, bạn cần:
Ví dụ minh họa (giả định bài toán cụ thể):
Cho tam giác ABC. Gọi M là trung điểm của BC. Chứng minh rằng: overrightarrow{AM} = (overrightarrow{AB} +overrightarrow{AC})/2
Lời giải:
Vì M là trung điểm của BC, ta có: overrightarrow{BM} =overrightarrow{MC}. Do đó, overrightarrow{BC} = 2overrightarrow{BM}.
Ta có: overrightarrow{AM} =overrightarrow{AB} +overrightarrow{BM}. Thay overrightarrow{BM} = (1/2)overrightarrow{BC} vào, ta được: overrightarrow{AM} =overrightarrow{AB} + (1/2)overrightarrow{BC}.
Mà overrightarrow{BC} =overrightarrow{AC} -overrightarrow{AB}, nên overrightarrow{AM} =overrightarrow{AB} + (1/2)(overrightarrow{AC} -overrightarrow{AB}) =overrightarrow{AB} + (1/2)overrightarrow{AC} - (1/2)overrightarrow{AB} = (1/2)overrightarrow{AB} + (1/2)overrightarrow{AC} = (overrightarrow{AB} +overrightarrow{AC})/2. Vậy, overrightarrow{AM} = (overrightarrow{AB} +overrightarrow{AC})/2 (đpcm).
Ngoài bài 43, SBT Toán 10 Cánh Diều còn có nhiều bài tập tương tự về vectơ. Để giải các bài tập này, bạn có thể áp dụng các phương pháp sau:
Khi giải bài tập về vectơ, bạn cần lưu ý những điều sau:
Hy vọng rằng với lời giải chi tiết và các hướng dẫn trên, bạn đã có thể giải bài 43 trang 61 SBT Toán 10 Cánh Diều một cách dễ dàng và hiệu quả. Hãy luyện tập thêm nhiều bài tập tương tự để nắm vững kiến thức về vectơ và áp dụng chúng vào các bài toán thực tế.