Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập trong sách bài tập Toán 10 Cánh Diều. Bài viết này sẽ hướng dẫn bạn từng bước giải bài 26 trang 32, giúp bạn hiểu rõ bản chất của bài toán và áp dụng kiến thức vào các bài tập tương tự.
Chúng tôi luôn cố gắng cung cấp nội dung chất lượng cao, chính xác và cập nhật nhất để hỗ trợ bạn trong quá trình học tập môn Toán.
Biểu diễn miền nghiệm của các hệ bất phương trình sau:
Đề bài
Biểu diễn miền nghiệm của các hệ bất phương trình sau:
a) \(\left\{ {\begin{array}{*{20}{c}}{x - 3y < 0}\\{x + 2y > - 3}\\{x + y < 2}\end{array}} \right.\) b) \(\left\{ {\begin{array}{*{20}{c}}{x - 2y \le 3}\\{3x + 2y \ge 9}\\{x + y \le 6}\\{x \ge 1}\end{array}} \right.\) c) \(\left\{ {\begin{array}{*{20}{c}}{x + 2y \le 2}\\{x + 2y \ge - 2}\\{x - 2y \le 2}\\{x - 2y \ge - 2}\end{array}} \right.\)
Phương pháp giải - Xem chi tiết
Xác định miền nghiệm của từng bpt. Miền nghiệm của hệ bpt là miền giao của các miền nghiệm ấy.
Biểu diễn miền nghiệm của bpt \(ax + by < c\)
Bước 1: Vẽ đường thẳng \(d:ax + by = c\)
Bước 2: Lấy một điểm \(M\left( {{x_o};{y_o}} \right)\) không thuộc d (ta thường lấy gốc tọa độ O nếu \(c \ne 0\)). Tính \(a{x_o} + b{y_o}\) và so sánh với c
Bước 3: Kết luận
Nếu \(a{x_o} + b{y_o} < c\)thì nửa mặt phẳng (không kể đường thẳng d) chứa điểm M là miền nghiệm của bất phương trình \(ax + by < c\)
Nếu \(a{x_o} + b{y_o} > c\) thì nửa mặt phẳng (không kể d) không chứa điểm M là miền nghiệm của bất phương trình \(ax + by > c\)
Lời giải chi tiết
a) Vẽ các đường thẳng:
\({d_1}{\rm{:}}\;x--3y = 0\) đi qua hai điểm có tọa độ (0; 0) và (3; 1).
\({d_2}{\rm{:}}\;x + 2y = - 3\) đi qua hai điểm có tọa độ (– 3; 0) và (1; – 2).
\({d_3}{\rm{:}}\;x + y = 2\) đi qua hai điểm có tọa độ (2; 0) và (0; 2).
Xét điểm A(1;0), không thuộc \({d_1},{d_2},{d_3}.\)
\(1 - 3.0 = 1 > 0 \Rightarrow A(1;0)\) không thuộc miền nghiệm của BPT \(x - 3y < 0\)
\(1 + 2.0 = 1 > - 3 \Rightarrow A(1;0)\) thuộc miền nghiệm của BPT \(x + 2y > - 3\)
\(1 + 0 = 1 < 2 \Rightarrow A(1;0)\) thuộc miền nghiệm của BPT \(x + y < 2\)
Biểu diễn miền nghiệm của từng bpt và gạch bỏ các miền không là nghiệm, ta được:
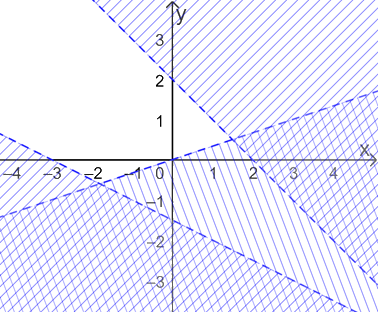
Miền nghiệm của hệ bpt là miền không gạch (không kể các bờ) trong hình trên.
b) Vẽ các đường thẳng:
d1: x – 2y = 3 đi qua hai điểm có tọa độ là (3; 0) và (1; – 1).
d2: 3x + 2y = 9 đi qua hai điểm (3; 0) và (1; 3).
d3: x + y = 6 đi qua hai điểm (6; 0) và (0; 6).
d4: x = 1 song song với trục tung và đi qua điểm (1; 0).
Xét điểm O(0;0), không thuộc \({d_1},{d_2},{d_3},{d_4}.\)
\(0 - 2.0 = 0 \le 3 \Rightarrow O(0;0)\) thuộc miền nghiệm của BPT \(x - 2y \le 3\)
\(3.0 + 2.0 < 9 \Rightarrow O(0;0)\) không thuộc miền nghiệm của BPT \(3x + 2y \ge 9\)
\(0 + 0 = 0 \le 6 \Rightarrow O(0;0)\) thuộc miền nghiệm của BPT \(x + y \le 6\)
\(0 < 1 \Rightarrow O(0;0)\) không thuộc miền nghiệm của BPT \(x \ge 1\)
Biểu diễn miền nghiệm của từng bpt và gạch bỏ các miền không là nghiệm, ta được:
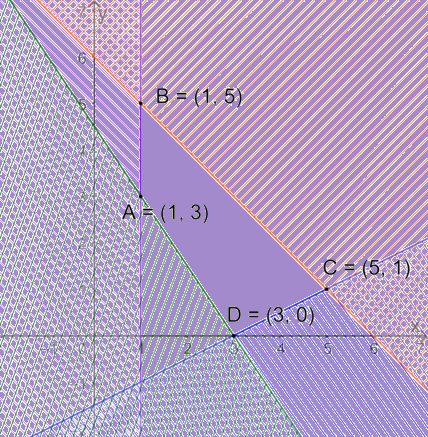
Miền nghiệm của hệ BPT là miền tứ giác ABCD (kể cả các cạnh) với A(1;3), B(1;5), C(5;1), D(3;0).
c) Vẽ các đường thẳng:
d1: x + 2y = 2 đi qua hai điểm có tọa độ là (2; 0) và (0; 1).
d2: x + 2y = – 2 đi qua hai điểm có tọa độ là (– 2; 0) và (0; – 1).
d3: x – 2y = 2 đi qua hai điểm có tọa độ là (2; 0) và (0; – 1).
d4: x – 2y = – 2 đi qua hai điểm có tọa độ là (–2; 0) và (0; 1).
Xét điểm O(0;0), không thuộc \({d_1},{d_2},{d_3},{d_4}.\)
\(0 + 2.0 = 0 \le 2 \Rightarrow O(0;0)\) thuộc miền nghiệm của BPT \(x + 2y \le 2\)
\(0 + 2.0 = 0 \ge - 2 \Rightarrow O(0;0)\) thuộc miền nghiệm của BPT \(x + 2y \ge - 2\)
\(0 - 2.0 = 0 \le 2 \Rightarrow O(0;0)\) thuộc miền nghiệm của BPT \(x - 2y \le 2\)
\(0 - 2.0 = 0 \ge - 2 \Rightarrow O(0;0)\) thuộc miền nghiệm của BPT \(x - 2y \ge - 2\)
Như vậy O(0;0) thuộc miền nghiệm của hệ bpt.
Biểu diễn miền nghiệm của từng bpt và gạch bỏ các miền không là nghiệm, ta được:
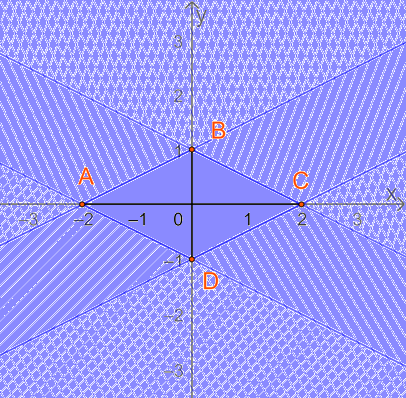
Miền nghiệm của hệ BPT là miền tứ giác ABCD (kể cả các cạnh) với A(-2;0), B(0;1), C(2;0), D(0;-1).
Bài 26 trang 32 SBT Toán 10 Cánh Diều thuộc chương trình học về vectơ trong mặt phẳng. Bài tập này thường yêu cầu học sinh vận dụng các kiến thức về phép cộng, phép trừ vectơ, tích của một số với vectơ, và các tính chất của các phép toán này để giải quyết các bài toán liên quan đến hình học và đại số.
Bài 26 thường bao gồm các dạng bài tập sau:
Để giải bài 26 trang 32 SBT Toán 10 Cánh Diều một cách hiệu quả, bạn cần nắm vững các kiến thức cơ bản về vectơ và các phép toán với vectơ. Dưới đây là hướng dẫn chi tiết cho từng dạng bài tập:
Để tính toán các phép toán với vectơ, bạn cần sử dụng các quy tắc sau:
Để chứng minh đẳng thức vectơ, bạn có thể sử dụng các phương pháp sau:
Để xác định điểm thỏa mãn một điều kiện cho trước liên quan đến vectơ, bạn có thể sử dụng các phương pháp sau:
Để ứng dụng vectơ vào giải quyết các bài toán hình học, bạn cần:
Để củng cố kiến thức về bài 26 trang 32 SBT Toán 10 Cánh Diều, bạn có thể làm thêm các bài tập sau:
Bài 26 trang 32 SBT Toán 10 Cánh Diều là một bài tập quan trọng giúp bạn rèn luyện kỹ năng vận dụng kiến thức về vectơ vào giải quyết các bài toán thực tế. Hy vọng rằng với hướng dẫn chi tiết này, bạn sẽ giải quyết bài tập một cách dễ dàng và hiệu quả.