Bài 8 trang 75 SBT Toán 10 Cánh Diều là một bài tập quan trọng trong chương trình học Toán 10, tập trung vào việc rèn luyện kỹ năng về vectơ và các phép toán vectơ. Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài tập này, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Chúng tôi cung cấp không chỉ đáp án mà còn cả phương pháp giải, giúp các em hiểu rõ bản chất của bài toán và áp dụng vào các tình huống khác nhau.
Cho hình bình hành ABCD có \(AB = a,BC = b,AC = m,BD = n\). Chứng minh \({m^2} + {n^2} = 2({a^2} + {b^2})\)
Đề bài
Cho hình bình hành ABCD có \(AB = a,BC = b,AC = m,BD = n\). Chứng minh \({m^2} + {n^2} = 2({a^2} + {b^2})\)
Phương pháp giải - Xem chi tiết
Bước 1: Sử dụng định lí cosin cho hai tam giác ∆ABC và ∆ADB để tính độ dài AC và BD
Bước 2: Xét mối liên hệ của các góc trong hình bình hành
Bước 3: Biến đổi các đẳng thức. Kết luận
Lời giải chi tiết
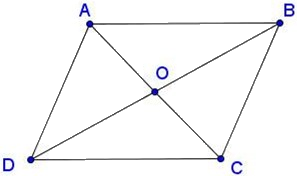
- Áp dụng định lí cosin cho ∆ABC ta có:
\(A{C^2} = A{B^2} + B{C^2} - 2.AB.BC.\cos \widehat {ABC}\)\( \Leftrightarrow {m^2} = {a^2} + {b^2} - 2ab.\cos \widehat {ABC}\) (1)
- Áp dụng định lí cosin cho ∆ADB ta có:
\(B{D^2} = A{B^2} + A{D^2} - 2.AB.AD.\cos \widehat {DAB}\)\( \Leftrightarrow {n^2} = {a^2} + {b^2} - 2ab.\cos \widehat {DAB}\) (2)
Do ABCD là hình bình hành nên AD // BC \( \Rightarrow \widehat {ABC} + \widehat {DAB} = {180^0}\) \( \Rightarrow \cos \widehat {ABC} = - \cos \widehat {DAB}\) (3)
Từ (1), (2), (3) ta có: \({m^2} + {n^2} = 2({a^2} + {b^2}) - 2ab(\cos \widehat {ABC} + \cos \widehat {DAB})\)\( \Leftrightarrow {m^2} + {n^2} = 2({a^2} + {b^2})\) (ĐPCM)
Bài 8 trang 75 SBT Toán 10 Cánh Diều yêu cầu học sinh vận dụng kiến thức về vectơ, đặc biệt là các phép toán cộng, trừ vectơ, nhân vectơ với một số thực và tích vô hướng của hai vectơ để giải quyết các bài toán hình học. Để giải quyết bài toán này một cách hiệu quả, chúng ta cần nắm vững các khái niệm cơ bản và các quy tắc liên quan.
Trước khi bắt tay vào giải bài toán, chúng ta cần đọc kỹ đề bài, xác định các yếu tố đã cho và yêu cầu của bài toán. Sau đó, chúng ta cần phân tích mối quan hệ giữa các yếu tố này và tìm ra hướng giải quyết phù hợp. Thông thường, bài toán vectơ có thể được giải bằng cách sử dụng các phép toán vectơ để biểu diễn các yếu tố hình học và sau đó áp dụng các công thức liên quan để tính toán.
(Ở đây sẽ là lời giải chi tiết cho từng ý của bài 8, bao gồm các bước giải, giải thích rõ ràng và sử dụng hình vẽ minh họa nếu cần thiết. Ví dụ:)
a) Ý a: Cho hình bình hành ABCD. Gọi M là trung điểm của BC. Hãy biểu diễn vectơ AM theo hai vectơ AB và AD.
Lời giải:
b) Ý b: Cho tam giác ABC. Gọi G là trọng tâm của tam giác. Hãy biểu diễn vectơ AG theo hai vectơ AB và AC.
Lời giải:
Sau khi đã giải xong bài toán, chúng ta có thể mở rộng kiến thức bằng cách giải các bài tập tương tự. Điều này sẽ giúp chúng ta củng cố kiến thức và rèn luyện kỹ năng giải toán. Một số bài tập tương tự có thể là:
Để giải bài tập vectơ một cách hiệu quả, chúng ta cần lưu ý một số điều sau:
Bài 8 trang 75 SBT Toán 10 Cánh Diều là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về vectơ và các phép toán vectơ. Bằng cách nắm vững lý thuyết, phân tích bài toán và áp dụng các phương pháp giải phù hợp, chúng ta có thể giải quyết bài toán này một cách hiệu quả. Hy vọng rằng, với hướng dẫn chi tiết này, các em học sinh sẽ tự tin hơn trong việc học tập môn Toán.
Giaitoan.edu.vn luôn đồng hành cùng các em trên con đường chinh phục môn Toán. Chúc các em học tập tốt!