Chào mừng các em học sinh đến với lời giải chi tiết bài 1 trang 68 sách bài tập Toán 11 - Chân trời sáng tạo tập 2. Bài viết này sẽ cung cấp cho các em phương pháp giải bài tập một cách dễ hiểu và hiệu quả.
Giaitoan.edu.vn luôn đồng hành cùng các em trong quá trình học tập, giúp các em nắm vững kiến thức và đạt kết quả tốt nhất.
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, cạnh bên SA vuông góc với đáy. Tính khoảng cách từ điểm A đến mặt phẳng (SBC) theo a, biết \(SA = \frac{{a\sqrt 6 }}{2}\).
Đề bài
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, cạnh bên SA vuông góc với đáy. Tính khoảng cách từ điểm A đến mặt phẳng (SBC) theo a, biết \(SA = \frac{{a\sqrt 6 }}{2}\).
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về khoảng cách từ điểm đến mặt phẳng để tính: Nếu H là hình chiếu vuông góc của điểm M trên mặt phẳng (P) thì độ dài đoạn thẳng MH được gọi là khoảng cách từ điểm M đến (P), kí hiệu d(M; (P)).
Lời giải chi tiết
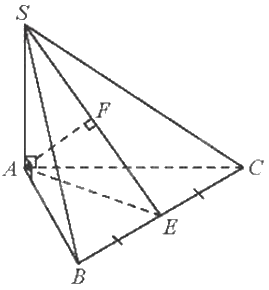
Gọi E là trung điểm của BC. Vì tam giác ABC đều nên AE là đường trung tuyến đồng thời là đường cao. Do đó, \(AE \bot BC\)
Ta có: \(SA \bot \left( {ABC} \right),BC \subset \left( {ABC} \right) \Rightarrow SA \bot BC\), mà \(AE \bot BC\). Suy ra: \(BC \bot \left( {SAE} \right)\)
Kẻ \(AF \bot SE\left( {S \in SE} \right)\). Vì \(BC \bot \left( {SAE} \right)\)\( \Rightarrow BC \bot AF\)
Ta có: \(BC \bot AF,AF \bot SE,\) BC và SE cắt nhau tại E và nằm trong mặt phẳng (SBC) nên \(AF \bot \left( {SBC} \right)\). Khi đó, AF là khoảng cách từ A đến mặt phẳng (SBC).
Vì tam giác ABC đều nên \(\widehat {ABC} = {60^0}\).
Tam giác ABE vuông tại E có: \(AE = AB.\sin \widehat {ABC} = \frac{{a\sqrt 3 }}{2}\)
Vì \(SA \bot \left( {ABC} \right),AE \subset \left( {ABC} \right) \Rightarrow SA \bot AE\)
Tam giác AES vuông tại A, có AF là đường cao nên:
\(\frac{1}{{A{F^2}}} = \frac{1}{{A{E^2}}} + \frac{1}{{S{A^2}}} = \frac{4}{{3{a^2}}} + \frac{4}{{6{a^2}}} = \frac{2}{{{a^2}}} \Rightarrow AF = \frac{{a\sqrt 2 }}{2}\)
Bài 1 trang 68 sách bài tập Toán 11 - Chân trời sáng tạo tập 2 thuộc chương trình học về phép biến hình. Bài tập này yêu cầu học sinh vận dụng kiến thức về phép tịnh tiến, phép quay, phép đối xứng trục và phép đối xứng tâm để giải quyết các bài toán thực tế. Việc nắm vững các khái niệm và tính chất của các phép biến hình là vô cùng quan trọng để giải quyết bài tập này một cách hiệu quả.
Bài 1 bao gồm các câu hỏi và bài tập nhỏ, yêu cầu học sinh:
Để giải câu a, ta cần xác định ảnh của điểm M qua phép tịnh tiến theo vectơ v. Sử dụng công thức: M' = M + v, ta sẽ tìm được tọa độ của điểm M'.
Đối với câu b, ta cần tìm tâm của phép quay biến điểm A thành điểm A'. Sử dụng công thức tìm tâm quay, ta sẽ xác định được tọa độ của tâm quay O.
Câu c yêu cầu chứng minh tam giác ABC là ảnh của tam giác A'B'C' qua phép đối xứng trục Oy. Để chứng minh điều này, ta cần chứng minh rằng mỗi đỉnh của tam giác ABC là ảnh của một đỉnh tương ứng của tam giác A'B'C' qua phép đối xứng trục Oy.
Để giải quyết các bài tập về phép biến hình một cách hiệu quả, các em cần:
Ví dụ: Cho điểm A(1; 2) và vectơ v = (3; -1). Tìm ảnh A' của điểm A qua phép tịnh tiến theo vectơ v.
Lời giải: A' = A + v = (1 + 3; 2 - 1) = (4; 1).
Khi giải bài tập về phép biến hình, các em cần chú ý:
Để củng cố kiến thức, các em có thể tự giải các bài tập tương tự trong sách bài tập và các tài liệu tham khảo khác.
Bài 1 trang 68 sách bài tập Toán 11 - Chân trời sáng tạo tập 2 là một bài tập quan trọng giúp các em hiểu sâu hơn về các phép biến hình. Hy vọng với lời giải chi tiết và phương pháp giải bài tập được trình bày trong bài viết này, các em sẽ tự tin hơn khi giải quyết các bài toán tương tự.