Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 5 trang 51 sách bài tập Toán 11 Chân trời sáng tạo tập 2. Bài viết này sẽ cung cấp đáp án, phương pháp giải và các kiến thức liên quan để giúp bạn hiểu rõ hơn về nội dung bài học.
Chúng tôi luôn cố gắng trình bày lời giải một cách dễ hiểu, logic và đầy đủ, phù hợp với trình độ của học sinh lớp 11. Hãy cùng theo dõi và luyện tập để nắm vững kiến thức Toán học nhé!
Cho tứ diện đều ABCD cạnh a. Gọi O là tâm đường tròn ngoại tiếp tam giác BCD. Chứng minh rằng hai đường thẳng OA và CD vuông góc với nhau.
Đề bài
Cho tứ diện đều ABCD cạnh a. Gọi O là tâm đường tròn ngoại tiếp tam giác BCD. Chứng minh rằng hai đường thẳng OA và CD vuông góc với nhau.
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về hai đường thẳng vuông góc trong không gian.
Lời giải chi tiết
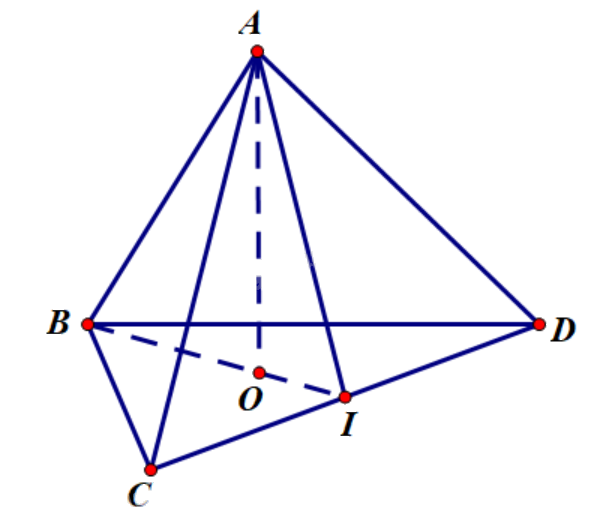
Gọi I là trung điểm của CD.
Tứ diện đều có 4 mặt là tam giác đều.
Vì O là tâm đường tròn ngoại tiếp tam giác BCD nên O là trọng tâm tam giác BCD.
Ta có AI vừa là đường trung tuyến, vừa là đường cao của tam giác ACD; BI vừa là đường trung tuyến, vừa là đường cao của tam giác BCD (do đó O thuộc BI vì trọng tâm nằm trên đường trung tuyến).
Khi đó, \(AI \bot CD\) và \(BI \bot CD\).
Suy ra \(CD \bot (ABI)\), mà OA thuộc (ABI) nên \(CD \bot OA\).
Bài 5 trang 51 sách bài tập Toán 11 Chân trời sáng tạo tập 2 thuộc chương trình học về đạo hàm. Bài tập này tập trung vào việc vận dụng các quy tắc tính đạo hàm của hàm số, đặc biệt là đạo hàm của tổng, hiệu, tích, thương của các hàm số. Việc nắm vững các quy tắc này là nền tảng quan trọng để giải quyết các bài toán phức tạp hơn trong chương trình học.
Bài 5 bao gồm các câu hỏi yêu cầu học sinh:
Để giúp các em học sinh hiểu rõ hơn về cách giải bài tập này, chúng tôi xin trình bày lời giải chi tiết cho từng câu hỏi:
Áp dụng quy tắc đạo hàm của tổng, hiệu và lũy thừa, ta có:
f'(x) = 3x^2 + 4x - 5
Áp dụng quy tắc đạo hàm của tích, ta có:
g'(x) = (2x)(x - 2) + (x^2 + 1)(1) = 2x^2 - 4x + x^2 + 1 = 3x^2 - 4x + 1
Áp dụng quy tắc đạo hàm của thương, ta có:
h'(x) = [(1)(x - 1) - (x + 1)(1)] / (x - 1)^2 = (x - 1 - x - 1) / (x - 1)^2 = -2 / (x - 1)^2
Để giải bài tập về đạo hàm một cách hiệu quả, các em cần lưu ý những điều sau:
Đạo hàm có rất nhiều ứng dụng trong thực tế, ví dụ như:
Bài 5 trang 51 sách bài tập Toán 11 Chân trời sáng tạo tập 2 là một bài tập quan trọng giúp các em học sinh củng cố kiến thức về đạo hàm. Hy vọng rằng với lời giải chi tiết và các lưu ý trên, các em sẽ giải quyết bài tập này một cách dễ dàng và hiệu quả. Chúc các em học tập tốt!
| Quy tắc | Công thức |
|---|---|
| Đạo hàm của hằng số | (c)' = 0 |
| Đạo hàm của lũy thừa | (x^n)' = nx^(n-1) |
| Đạo hàm của tổng/hiệu | (u ± v)' = u' ± v' |
| Đạo hàm của tích | (uv)' = u'v + uv' |
| Đạo hàm của thương | (u/v)' = (u'v - uv') / v^2 |