Bài 10 trang 68 Sách bài tập Toán 11 Chân trời sáng tạo tập 2 là một bài tập quan trọng trong chương trình học. Bài tập này yêu cầu học sinh vận dụng kiến thức về đạo hàm để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 10 trang 68, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Tính thể tích của một cái sọt đựng đồ có dạng hình chóp cụt tứ giác đều, đáy lớn có cạnh bằng 80cm, đáy nhỏ có cạnh bằng 40cm và cạnh bên bằng 80cm.
Đề bài
Tính thể tích của một cái sọt đựng đồ có dạng hình chóp cụt tứ giác đều, đáy lớn có cạnh bằng 80cm, đáy nhỏ có cạnh bằng 40cm và cạnh bên bằng 80cm.

Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về thể tích khối chóp cụt đều có chiều cao h và diện tích hai đáy S, S’ là: \(V = \frac{1}{3}h\left( {S + \sqrt {SS'} + S'} \right)\)
Lời giải chi tiết
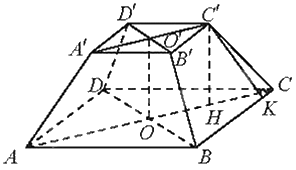
Đặt tên các điểm như hình vẽ. Khi đó ta có: \(OC = 40\sqrt 2 ,O'C' = 20\sqrt 2 \Rightarrow CH = 20\sqrt 2 \)
Tam giác C’CH vuông tại H có: \(C'H = \sqrt {CC{'^2} - C{H^2}} = 20\sqrt {14} \)
Do đó, \(O'O = C'H = 20\sqrt {14} \)
Thể tích cái sọt đựng đồ là:
\(V = \frac{1}{3}.20\sqrt {14} .\left( {6400 + \sqrt {6400.1600} + 1600} \right) \approx 279377,08\left( {c{m^3}} \right)\)
Bài 10 trang 68 Sách bài tập Toán 11 Chân trời sáng tạo tập 2 thuộc chương trình học về đạo hàm của hàm số. Bài tập này tập trung vào việc tính đạo hàm của các hàm số lượng giác và hàm hợp. Việc nắm vững kiến thức về đạo hàm là nền tảng quan trọng để giải quyết các bài toán liên quan đến tối ưu hóa, tìm cực trị và nghiên cứu sự biến thiên của hàm số.
Bài 10 trang 68 bao gồm một số câu hỏi nhỏ, yêu cầu học sinh:
Để giúp học sinh hiểu rõ hơn về cách giải bài tập này, chúng ta sẽ đi vào phân tích từng câu hỏi cụ thể:
Để tính đạo hàm của hàm số y = sin(2x + 1), ta sử dụng quy tắc đạo hàm của hàm hợp: (u(v(x)))' = u'(v(x)) * v'(x).
Trong trường hợp này, u(v) = sin(v) và v(x) = 2x + 1.
Ta có: u'(v) = cos(v) và v'(x) = 2.
Vậy, y' = cos(2x + 1) * 2 = 2cos(2x + 1).
Tương tự như câu a, ta sử dụng quy tắc đạo hàm của hàm hợp.
Trong trường hợp này, u(v) = cos(v) và v(x) = x^2.
Ta có: u'(v) = -sin(v) và v'(x) = 2x.
Vậy, y' = -sin(x^2) * 2x = -2xsin(x^2).
Áp dụng quy tắc đạo hàm của hàm hợp, ta có:
u(v) = tan(v) và v(x) = 3x - 2.
u'(v) = 1/cos^2(v) = sec^2(v) và v'(x) = 3.
Vậy, y' = sec^2(3x - 2) * 3 = 3sec^2(3x - 2).
Ngoài các công thức đạo hàm cơ bản, học sinh cần nắm vững các quy tắc đạo hàm khác như quy tắc tích, quy tắc thương và quy tắc đạo hàm hàm ẩn. Việc luyện tập thường xuyên với các bài tập đa dạng sẽ giúp học sinh củng cố kiến thức và nâng cao kỹ năng giải toán.
Đạo hàm có rất nhiều ứng dụng trong thực tế, bao gồm:
Bài 10 trang 68 Sách bài tập Toán 11 Chân trời sáng tạo tập 2 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng tính đạo hàm và áp dụng các công thức đạo hàm vào giải quyết các bài toán thực tế. Hy vọng với lời giải chi tiết và những kiến thức mở rộng trên, các em học sinh sẽ tự tin hơn trong quá trình học tập.
| Hàm số | Đạo hàm |
|---|---|
| y = sin(x) | y' = cos(x) |
| y = cos(x) | y' = -sin(x) |
| y = tan(x) | y' = sec^2(x) |