Bài 6 trang 100 sách bài tập Toán 11 Chân trời sáng tạo tập 2 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số. Bài tập này thường yêu cầu học sinh tính đạo hàm, tìm cực trị, và vẽ đồ thị hàm số.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 6 trang 100, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Châu gieo một con xúc xắc cân đối và đồng chất liên tiếp cho đến khi xuất hiện mặt 6 chấm thì dừng lại. Sử dụng sơ đồ hình cây, tính xác suất của biến cố “Châu phải gieo không quá ba lần để xuất hiện mặt 6 chấm”.
Đề bài
Châu gieo một con xúc xắc cân đối và đồng chất liên tiếp cho đến khi xuất hiện mặt 6 chấm thì dừng lại. Sử dụng sơ đồ hình cây, tính xác suất của biến cố “Châu phải gieo không quá ba lần để xuất hiện mặt 6 chấm”.
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về sơ đồ hình cây để tính xác suất.
Lời giải chi tiết
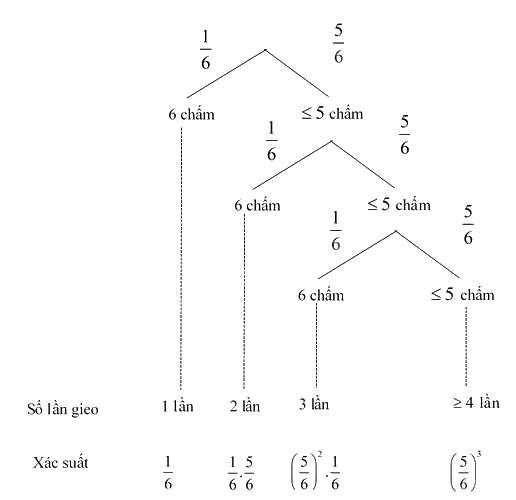
Xác suất của biến cố “Châu phải gieo không quá ba lần để xuất hiện mặt 6 chấm” là:
\(\frac{1}{6} + \frac{5}{6}.\frac{1}{6} + {\left( {\frac{5}{6}} \right)^2}.\frac{1}{6} = \frac{{91}}{{216}}\)
Bài 6 trong sách bài tập Toán 11 Chân trời sáng tạo tập 2 tập trung vào việc vận dụng các kiến thức về đạo hàm để giải quyết các bài toán thực tế liên quan đến sự biến thiên của hàm số. Để giải quyết bài toán này một cách hiệu quả, học sinh cần nắm vững các bước sau:
Để minh họa phương pháp giải, chúng ta sẽ cùng nhau phân tích và giải chi tiết bài 6 trang 100 sách bài tập Toán 11 Chân trời sáng tạo tập 2. (Giả sử bài 6 là hàm số y = x^3 - 3x^2 + 2)
Đạo hàm bậc nhất của hàm số y = x^3 - 3x^2 + 2 là:
y' = 3x^2 - 6x
Đạo hàm bậc hai của hàm số y = x^3 - 3x^2 + 2 là:
y'' = 6x - 6
Giải phương trình y' = 0:
3x^2 - 6x = 0
3x(x - 2) = 0
Vậy, x = 0 hoặc x = 2
Các điểm cực trị là x = 0 và x = 2.
Giải phương trình y'' = 0:
6x - 6 = 0
x = 1
Điểm uốn là x = 1.
Dựa vào các thông tin đã tìm được, ta có thể vẽ đồ thị hàm số y = x^3 - 3x^2 + 2. Đồ thị hàm số có điểm cực đại tại x = 0, điểm cực tiểu tại x = 2 và điểm uốn tại x = 1.
Ngoài bài 6, sách bài tập Toán 11 Chân trời sáng tạo tập 2 còn nhiều bài tập tương tự về khảo sát hàm số bằng đạo hàm. Để giải nhanh các bài tập này, học sinh nên:
Bài 6 trang 100 sách bài tập Toán 11 Chân trời sáng tạo tập 2 là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm và ứng dụng của đạo hàm trong việc khảo sát hàm số. Hy vọng với lời giải chi tiết và phương pháp giải hiệu quả mà Giaitoan.edu.vn cung cấp, các em học sinh sẽ tự tin hơn trong việc giải quyết các bài tập tương tự.