Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho bài 5 trang 62 sách bài tập Toán 11 - Chân trời sáng tạo tập 2. Bài viết này sẽ giúp bạn nắm vững kiến thức và kỹ năng giải toán, tự tin hơn trong quá trình học tập.
Chúng tôi hiểu rằng việc giải các bài tập toán đôi khi có thể gặp khó khăn. Vì vậy, đội ngũ giáo viên giàu kinh nghiệm của giaitoan.edu.vn đã biên soạn lời giải chi tiết, từng bước, giúp bạn hiểu rõ phương pháp và cách tiếp cận bài toán.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, \(SA = a\sqrt 3 \). Hai mặt phẳng (SAB) và (SAD) cùng vuông góc với mặt đáy.
Đề bài
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, \(SA = a\sqrt 3 \). Hai mặt phẳng (SAB) và (SAD) cùng vuông góc với mặt đáy. Gọi \(\left( \alpha \right)\) là mặt phẳng qua AB và vuông góc với mặt phẳng (SCD).
a) Tìm các giao tuyến của mặt phẳng \(\left( \alpha \right)\) với các mặt của hình chóp.
b) Các giao tuyến ở câu a tạo thành hình gì? Tính diện tích của hình đó.
Phương pháp giải - Xem chi tiết
+ Sử dụng kiến thức về điều kiện để hai mặt phẳng vuông góc: Điều kiện cần và đủ để hai mặt phẳng vuông góc là mặt phẳng này chứa một đường thẳng vuông góc với mặt phẳng kia.
+ Sử dụng kiến thức về tính chất cơ bản của hai mặt phẳng vuông góc: Nếu hai mặt phẳng vuông góc với nhau mặt phẳng thứ ba thì giao tuyến của chúng vuông góc với mặt phẳng thứ ba.
Lời giải chi tiết
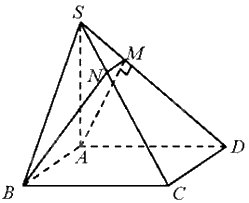
a) Vì mặt phẳng (SAB) và (SAD) cùng vuông góc với mặt đáy, SA là giao tuyến của hai mặt phẳng (SAB) và (SAD) nên \(SA \bot \left( {ABCD} \right)\)
Vì ABCD là hình vuông nên \(AD \bot DC\).
Mà \(SA \bot \left( {ABCD} \right),DC \subset \left( {ABCD} \right) \) \( \Rightarrow SA \bot DC\)
Do đó, \(DC \bot \left( {SAD} \right)\). Lại có: \(DC \subset \left( {SDC} \right) \) \( \Rightarrow \left( {SCD} \right) \bot \left( {SAD} \right)\)
Vẽ \(AM \bot SD\) tại M. Do đó, \(AM \bot \left( {SCD} \right)\). Suy ra, \(\left( {BAM} \right) \bot \left( {SCD} \right)\) hay (ABM) là mặt phẳng qua AB và vuông góc với mặt phẳng (SCD).
Trong mặt phẳng (SCD), kẻ MN//CD\(\left( {N \in SC} \right)\). Suy ra, MN//AB nên \(MN \subset \left( \alpha \right)\)
Khi đó, giao tuyến của \(\left( \alpha \right)\) với:
Mặt phẳng (ABCD) là AB.
Mặt phẳng (ABS) là AB.
Mặt phẳng (SBC) là NB.
Mặt phẳng (SCD) là MN.
Mặt phẳng (ASD) là AM.
b) Ta có: MN//AB, \(AB \bot AM\left( {do\;AB \bot \left( {SAD} \right)} \right)\) nên tứ giác ABNM là hình thang vuông tại A và M.
Tam giác SAD vuông tại A có AM là đường cao nên
\(\frac{1}{{A{M^2}}} = \frac{1}{{S{A^2}}} + \frac{1}{{A{D^2}}} = \frac{1}{{3{a^2}}} + \frac{1}{{{a^2}}} = \frac{4}{{3{a^2}}} \) \( \Rightarrow AM = \frac{{a\sqrt 3 }}{2}\)
Vì MN//CD nên \(\frac{{MN}}{{CD}} = \frac{{SM}}{{SD}} \) \( \Rightarrow \frac{{MN}}{{CD}} = \frac{{\frac{{S{A^2}}}{{SD}}}}{{SD}} = \frac{{S{A^2}}}{{S{D^2}}} = \frac{{S{A^2}}}{{S{A^2} + A{D^2}}} = \frac{{3{a^2}}}{{4{a^2}}} = \frac{3}{4}\)
Do đó, \(MN = \frac{3}{4}CD = \frac{3}{4}a\)
Vậy diện tích hình thang ABNM là: \(S = \frac{1}{2}AM\left( {MN + AB} \right) \) \(= \frac{1}{2}.\frac{{a\sqrt 3 }}{2}.\left( {\frac{3}{4}a + a} \right) = \frac{{7{a^2}\sqrt 3 }}{{16}}\)
Bài 5 trang 62 sách bài tập Toán 11 - Chân trời sáng tạo tập 2 thuộc chương trình học về đạo hàm. Bài tập này tập trung vào việc vận dụng các quy tắc tính đạo hàm của hàm số, đặc biệt là đạo hàm của tổng, hiệu, tích, thương của các hàm số. Việc nắm vững các quy tắc này là nền tảng quan trọng để giải quyết các bài toán phức tạp hơn trong chương trình học.
Bài 5 bao gồm một số câu hỏi nhỏ, yêu cầu học sinh tính đạo hàm của các hàm số cho trước. Các hàm số này có thể là các hàm số đơn giản như đa thức, hàm số lượng giác, hoặc các hàm số phức tạp hơn được tạo thành từ các hàm số đơn giản thông qua các phép toán cộng, trừ, nhân, chia.
Để hiểu rõ hơn về cách giải bài tập về đạo hàm, chúng ta hãy xem xét một ví dụ khác. Giả sử chúng ta cần tính đạo hàm của hàm số y = (sin(x) + 1)^2. Ta có thể sử dụng quy tắc đạo hàm của hàm hợp. Đặt u = sin(x) + 1, thì y = u^2. Khi đó, dy/dx = (dy/du) * (du/dx) = 2u * cos(x) = 2(sin(x) + 1) * cos(x).
Đạo hàm có rất nhiều ứng dụng trong thực tế, bao gồm:
Bài 5 trang 62 sách bài tập Toán 11 - Chân trời sáng tạo tập 2 là một bài tập quan trọng giúp học sinh củng cố kiến thức về đạo hàm. Bằng cách nắm vững các quy tắc đạo hàm cơ bản và luyện tập thường xuyên, bạn có thể tự tin giải quyết các bài toán về đạo hàm một cách hiệu quả. Hy vọng rằng bài viết này đã cung cấp cho bạn những thông tin hữu ích và giúp bạn hiểu rõ hơn về bài tập này.