Bài 13 trang 77 sách bài tập Toán 11 Chân trời sáng tạo tập 1 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về tổ hợp và xác suất. Bài tập này thường yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 13 trang 77, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
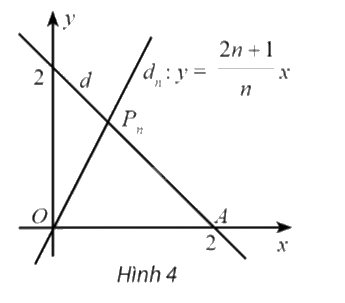
Trong mặt phẳng tọa độ Oxy, đường thẳng \(d:x + y = 2\) cắt trục hoành tại điểm A và cắt đường thẳng \({d_n}:y = \frac{{2n + 1}}{n}x\) tại điểm \({P_n}\left( {n \in \mathbb{N}*} \right)\). Kí hiệu \({S_n}\) là diện tích của tam giác \(OA{P_n}\). Tính \(\lim {S_n}\).
Đề bài
Trong mặt phẳng tọa độ Oxy, đường thẳng \(d:x + y = 2\) cắt trục hoành tại điểm A và cắt đường thẳng \({d_n}:y = \frac{{2n + 1}}{n}x\) tại điểm \({P_n}\left( {n \in \mathbb{N}*} \right)\). Kí hiệu \({S_n}\) là diện tích của tam giác \(OA{P_n}\). Tính \(\lim {S_n}\).
Phương pháp giải - Xem chi tiết
+ Sử dụng kiến thức về các phép toán về giới hạn hữu hạn của dãy số để tính: Cho \(\lim {u_n} = a,\lim {v_n} = b\) và c là hằng số: \(\lim \left( {{u_n} + {v_n}} \right) = a + b\), \(\lim \left( {c.{u_n}} \right) = c.a\), \(\lim \frac{{{u_n}}}{{{v_n}}} = \frac{a}{b}\left( {b \ne 0} \right)\).
+ Sử dụng kiến thức về một số giới hạn cơ bản để tính: \(\lim {q^n} = 0\) (q là số thực, \(\left| q \right| < 1\)), \(\lim c = c\) (c là hằng số).
Lời giải chi tiết
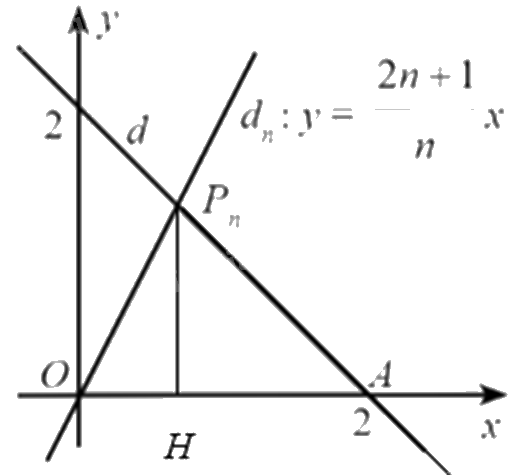
Ta có: \(A\left( {0;2} \right);OA = 2;\widehat {OA{P_n}} = {45^0}\)
Vì P là giao điểm của \({d_n}\) và d nên tọa độ của P là nghiệm của hệ phương trình:
\(\left\{ \begin{array}{l}x + y = 2\\y = \frac{{2n + 1}}{n}x\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x + \frac{{2n + 1}}{n}x = 2\\y = \frac{{2n + 1}}{n}x\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x.\frac{{3n + 1}}{n} = 2\\y = \frac{{2n + 1}}{n}x\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \frac{{2n}}{{3n + 1}}\\y = \frac{{4n + 2}}{{3n + 1}}\end{array} \right.\)
Do đó, \({P_n}\left( {\frac{{2n}}{{3n + 1}};\frac{{4n + 2}}{{3n + 1}}} \right)\)
Gọi H là hình chiếu vuông góc của \({P_n}\) trên trục Ox.
Khi đó: \({P_n}H = \left| {\frac{{4n + 2}}{{3n + 1}}} \right| = \frac{{4n + 2}}{{3n + 1}}\left( {do\;n \in \mathbb{N}*} \right)\)
Diện tích tam giác \(OA{P_n}\) là: \({S_n} = \frac{1}{2}.OA.{P_n}H = \frac{1}{2}.2.\frac{{4n + 2}}{{3n + 1}} = \frac{{4n + 2}}{{3n + 1}}\)
\(\lim {S_n} = \lim \frac{{4n + 2}}{{3n + 1}} = \lim \frac{{4 + \frac{2}{n}}}{{3 + \frac{1}{n}}} = \frac{4}{3}\)
Bài 13 trang 77 sách bài tập Toán 11 Chân trời sáng tạo tập 1 thuộc chương Tổ hợp và Xác suất, tập trung vào việc ứng dụng các công thức và quy tắc đếm để giải quyết các bài toán liên quan đến hoán vị, chỉnh hợp và tổ hợp. Bài tập này thường xuất hiện trong các kỳ thi và kiểm tra, do đó việc nắm vững phương pháp giải là vô cùng quan trọng.
Bài 13 thường bao gồm các dạng bài tập sau:
Để giúp các em học sinh hiểu rõ hơn về cách giải bài 13 trang 77, chúng ta sẽ đi vào phân tích từng phần của bài tập. (Ở đây sẽ là lời giải chi tiết cho từng câu của bài 13, bao gồm các bước giải, giải thích và kết luận. Ví dụ:)
Giải thích: ...
Kết luận: ...
Giải thích: ...
Kết luận: ...
Khi giải các bài tập về tổ hợp và xác suất, các em cần lưu ý những điều sau:
Để hiểu rõ hơn về cách áp dụng các công thức và quy tắc, chúng ta hãy xem xét một ví dụ minh họa:
Ví dụ: Có bao nhiêu cách sắp xếp 5 cuốn sách khác nhau lên một kệ sách?
Giải: Đây là một bài toán về hoán vị. Số cách sắp xếp 5 cuốn sách khác nhau là 5! = 5 x 4 x 3 x 2 x 1 = 120 cách.
Để học tập và ôn luyện kiến thức về tổ hợp và xác suất, các em có thể tham khảo các tài liệu sau:
Bài 13 trang 77 sách bài tập Toán 11 Chân trời sáng tạo tập 1 là một bài tập quan trọng giúp các em học sinh rèn luyện kỹ năng về tổ hợp và xác suất. Hy vọng với lời giải chi tiết và các lưu ý trên, các em sẽ tự tin hơn khi giải quyết các bài tập tương tự.