Bài 3 trang 112 sách bài tập Toán 11 Chân trời sáng tạo tập 1 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về tổ hợp và xác suất. Bài tập này yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 3 trang 112, giúp các em học sinh nắm vững kiến thức và tự tin làm bài tập.
Cho tứ diện ABCD. Gọi E, F, G lần lượt là các điểm thuộc ba cạnh AB, AC, BD sao cho EF cắt BC tại I, AD cắt EG tại H. Chứng minh rằng ba đường thẳng CD, IG, HF cùng đi qua một điểm.
Đề bài
Cho tứ diện ABCD. Gọi E, F, G lần lượt là các điểm thuộc ba cạnh AB, AC, BD sao cho EF cắt BC tại I, AD cắt EG tại H. Chứng minh rằng ba đường thẳng CD, IG, HF cùng đi qua một điểm.
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về chứng minh ba đường thẳng đồng quy để chứng minh ba đường thẳng đồng quy:
+ Gọi O là giao điểm của HF và IG
+ Chứng minh O thuộc CD.
Lời giải chi tiết
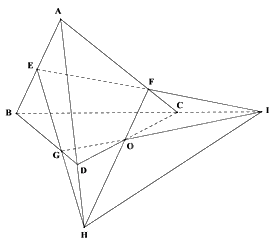
Gọi O là giao điểm của HF và IG.
Ta có: \(O \in HF\), mà \(HF \subset \left( {ACD} \right) \Rightarrow O \in \left( {ACD} \right)\)
Vì \(O \in IG\), mà \(IG \subset \left( {BCD} \right) \Rightarrow O \in \left( {BCD} \right)\)
Do đó, \(O \in \left( {BCD} \right) \cap \left( {ACD} \right)\)
Mặt khác, CD là giao tuyến của hai mặt phẳng (ACD) và (BCD)
Do đó, \(O \in CD\). Vậy ba đường thẳng CD, IG, HF cùng đi qua một điểm.
Bài 3 trong sách bài tập Toán 11 Chân trời sáng tạo tập 1 tập trung vào việc ứng dụng các kiến thức về hoán vị, chỉnh hợp và tổ hợp để giải quyết các bài toán đếm. Bài tập này thường xuất hiện trong các kỳ thi và kiểm tra, do đó việc nắm vững phương pháp giải là vô cùng quan trọng.
Bài 3 thường bao gồm các dạng bài tập sau:
Để giải quyết bài 3 trang 112 một cách hiệu quả, bạn cần:
Ví dụ: Có 5 người, trong đó có 2 nam và 3 nữ. Hỏi có bao nhiêu cách xếp 5 người này vào một hàng ngang sao cho hai người nam đứng cạnh nhau?
Giải:
Ta coi hai người nam như một khối. Khi đó, ta có 4 phần tử: khối hai người nam và 3 người nữ. Số cách sắp xếp 4 phần tử này là 4! = 24.
Trong khối hai người nam, có 2! = 2 cách sắp xếp.
Vậy, tổng số cách xếp là 4! * 2! = 24 * 2 = 48.
Để củng cố kiến thức và kỹ năng giải bài tập về hoán vị, chỉnh hợp và tổ hợp, bạn nên luyện tập thêm các bài tập tương tự trong sách bài tập và các tài liệu tham khảo khác.
Khi gặp khó khăn trong quá trình giải bài tập, đừng ngần ngại tìm kiếm sự giúp đỡ từ giáo viên, bạn bè hoặc các nguồn tài liệu trực tuyến. Việc hiểu rõ bản chất của bài toán và áp dụng đúng phương pháp giải là chìa khóa để thành công.
| Công thức | Mô tả |
|---|---|
| Pn | Số hoán vị của n phần tử: Pn = n! |
| Ank | Số chỉnh hợp chập k của n phần tử: Ank = n! / (n-k)! |
| Cnk | Số tổ hợp chập k của n phần tử: Cnk = n! / (k! * (n-k)!) |
Hy vọng với lời giải chi tiết và những hướng dẫn trên, các bạn học sinh sẽ tự tin hơn khi giải bài 3 trang 112 sách bài tập Toán 11 Chân trời sáng tạo tập 1. Chúc các bạn học tốt!