Giải bài 10 trang 9 sách bài tập Toán 11 - Chân trời sáng tạo tập 1

Giải bài 10 trang 9 sách bài tập toán 11 - Chân trời sáng tạo tập 1

Giải bài 10 trang 9 sách bài tập Toán 11 - Chân trời sáng tạo tập 1

Giaitoan.edu.vn xin giới thiệu lời giải chi tiết bài 10 trang 9 sách bài tập Toán 11 - Chân trời sáng tạo tập 1. Bài viết này sẽ cung cấp cho bạn các bước giải bài tập một cách rõ ràng, dễ hiểu, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.

Chúng tôi luôn cố gắng mang đến những giải pháp học tập hiệu quả nhất cho học sinh. Hãy cùng theo dõi bài viết để hiểu rõ hơn về cách giải bài tập này nhé!

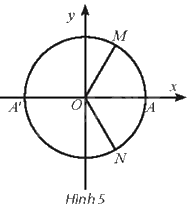
Trong hình bên, các điểm M, A’, N tạo thành ba đỉnh của một tam giác đều. Vị trí các điểm M, A’, N trên đường tròn lượng giác có thể được biểu diễn cho góc lượng giác nào sau đây?

Đề bài

\(\frac{\pi }{3} + k\frac{{2\pi }}{3}\left( {k \in \mathbb{Z}} \right); - \pi + k\frac{{2\pi }}{3}\left( {k \in \mathbb{Z}} \right); - \frac{\pi }{3} + k\frac{\pi }{3}\left( {k \in \mathbb{Z}} \right)\).

Giải bài 10 trang 9 sách bài tập toán 11 - Chân trời sáng tạo tập 1 1

Phương pháp giải - Xem chi tiết Giải bài 10 trang 9 sách bài tập toán 11 - Chân trời sáng tạo tập 1 2

Sử dụng kiến thức về biểu diễn góc lượng giác trên đường tròn lượng giác.

Lời giải chi tiết

+) Xét góc lượng giác \(\frac{\pi }{3} + k\frac{{2\pi }}{3}\left( {k \in \mathbb{Z}} \right)\):

Với \(k = 0\) thì ta có góc lượng giác \(\alpha = \frac{\pi }{3}\) biểu diễn là điểm M trên đường tròn lượng giác.

Với \(k = - 1\) thì ta có góc lượng giác \(\beta = - \frac{\pi }{3}\) biểu diễn là điểm N trên đường tròn lượng giác.

Với \(k = 1\) thì ta có góc lượng giác \(\gamma = \pi \) biểu diễn là điểm A’ trên đường tròn lượng giác.

Do đó, vị trí các điểm M, A’, N trên đường tròn lượng giác có thể biểu diễn cho góc lượng giác \(\frac{\pi }{3} + k\frac{{2\pi }}{3}\left( {k \in \mathbb{Z}} \right)\).

+) Xét góc lượng giác \( - \pi + k\frac{{2\pi }}{3}\left( {k \in \mathbb{Z}} \right)\):

Với \(k = 0\) thì ta có góc lượng giác \(\alpha = - \pi \) biểu diễn là điểm A’ trên đường tròn lượng giác

Với \(k = 1\) thì ta có góc lượng giác \(\beta = - \frac{\pi }{3}\) biểu diễn là điểm N trên đường tròn lượng giác

Với \(k = 2\) thì ta có góc lượng giác \(\gamma = \frac{\pi }{3}\) biểu diễn là điểm M trên đường tròn lượng giác

Do đó, vị trí các điểm M, A’, N trên đường tròn lượng giác có thể biểu diễn cho góc lượng giác \( - \pi + k\frac{{2\pi }}{3}\left( {k \in \mathbb{Z}} \right)\).

+) Xét góc lượng giác \( - \frac{\pi }{3} + k\frac{\pi }{3}\left( {k \in \mathbb{Z}} \right)\):

Với \(k = 1\) ta có góc lượng giác bằng 0, được biểu diễn bởi điểm A, không thỏa mãn yêu cầu bài toán.

Chinh phục Toán 11, mở rộng cánh cửa Đại học trong tầm tay! Khám phá ngay Giải bài 10 trang 9 sách bài tập toán 11 - Chân trời sáng tạo tập 1 – hành trang không thể thiếu trong chuyên mục Giải bài tập Toán 11 trên nền tảng học toán. Bộ bài tập toán thpt được biên soạn chuyên sâu, bám sát chặt chẽ chương trình Toán lớp 11 và định hướng các kỳ thi quan trọng, cam kết tối ưu hóa toàn diện quá trình ôn luyện. Qua đó, học sinh không chỉ làm chủ kiến thức phức tạp mà còn rèn luyện tư duy giải quyết vấn đề, sẵn sàng cho các kỳ thi và chương trình đại học, nhờ phương pháp tiếp cận trực quan, logic và hiệu quả học tập vượt trội!

Giải bài 10 trang 9 sách bài tập Toán 11 - Chân trời sáng tạo tập 1: Chi tiết và Dễ Hiểu

Bài 10 trang 9 sách bài tập Toán 11 - Chân trời sáng tạo tập 1 thuộc chương trình học về hàm số bậc hai. Để giải bài tập này, chúng ta cần nắm vững các kiến thức cơ bản về:

Định nghĩa hàm số bậc hai
Đồ thị hàm số bậc hai
Các yếu tố của đồ thị hàm số bậc hai (đỉnh, trục đối xứng, giao điểm với trục hoành, giao điểm với trục tung)
Cách xác định các yếu tố của đồ thị hàm số bậc hai

Nội dung bài tập:

Bài 10 yêu cầu xác định các hệ số a, b, c của hàm số bậc hai và vẽ đồ thị hàm số. Cụ thể, bài tập có thể yêu cầu:

Xác định a, b, c từ phương trình hàm số
Tìm tọa độ đỉnh của parabol
Tìm phương trình trục đối xứng
Tìm giao điểm của parabol với trục hoành (nếu có)
Tìm giao điểm của parabol với trục tung
Vẽ đồ thị hàm số dựa trên các thông tin đã tìm được

Hướng dẫn giải chi tiết:

Để giải bài tập này, chúng ta thực hiện theo các bước sau:

Bước 1: Xác định các hệ số a, b, c. Dựa vào phương trình hàm số đã cho, xác định chính xác giá trị của các hệ số a, b, c.
Bước 2: Tính tọa độ đỉnh của parabol. Sử dụng công thức x_đỉnh = -b/(2a) và y_đỉnh = f(x_đỉnh) để tính tọa độ đỉnh của parabol.
Bước 3: Tìm phương trình trục đối xứng. Phương trình trục đối xứng của parabol là x = x_đỉnh.
Bước 4: Tìm giao điểm với trục tung. Giao điểm với trục tung là điểm có hoành độ x = 0. Thay x = 0 vào phương trình hàm số để tìm tung độ y.
Bước 5: Tìm giao điểm với trục hoành (nếu có). Giải phương trình f(x) = 0 để tìm hoành độ của các giao điểm với trục hoành.
Bước 6: Vẽ đồ thị hàm số. Dựa vào các thông tin đã tìm được (đỉnh, trục đối xứng, giao điểm), vẽ đồ thị hàm số trên hệ trục tọa độ.

Ví dụ minh họa:

Giả sử hàm số có dạng y = x² - 4x + 3.

a = 1, b = -4, c = 3
x_đỉnh = -(-4)/(2*1) = 2
y_đỉnh = 2² - 4*2 + 3 = -1
Tọa độ đỉnh: (2, -1)
Trục đối xứng: x = 2
Giao điểm với trục tung: (0, 3)
Giao điểm với trục hoành: Giải phương trình x² - 4x + 3 = 0, ta được x = 1 và x = 3. Vậy giao điểm với trục hoành là (1, 0) và (3, 0).

Lưu ý quan trọng:

Khi vẽ đồ thị, cần chú ý đến dấu của hệ số a để xác định chiều mở của parabol (lên trên nếu a > 0, xuống dưới nếu a < 0).
Kiểm tra lại các kết quả tính toán để đảm bảo tính chính xác.
Sử dụng các công cụ vẽ đồ thị trực tuyến để kiểm tra lại kết quả vẽ đồ thị của mình.

Mở rộng kiến thức:

Ngoài việc giải bài tập, bạn nên tìm hiểu thêm về các ứng dụng của hàm số bậc hai trong thực tế, chẳng hạn như trong vật lý (quỹ đạo của vật ném), kỹ thuật (thiết kế cầu, đường cong) và kinh tế (mô hình lợi nhuận). Việc hiểu rõ các ứng dụng này sẽ giúp bạn thấy được tầm quan trọng và tính thực tiễn của kiến thức đã học.

Hy vọng với hướng dẫn chi tiết này, bạn đã có thể tự tin giải bài 10 trang 9 sách bài tập Toán 11 - Chân trời sáng tạo tập 1. Chúc bạn học tập tốt!