Chào mừng bạn đến với giaitoan.edu.vn, nơi cung cấp lời giải chi tiết và dễ hiểu cho các bài tập Toán 11. Bài viết này sẽ hướng dẫn bạn giải bài 5 trang 150 sách bài tập Toán 11 - Chân trời sáng tạo tập 1 một cách nhanh chóng và hiệu quả.
Chúng tôi luôn cố gắng mang đến những giải pháp học tập tốt nhất, giúp bạn nắm vững kiến thức và tự tin hơn trong quá trình học tập.
Bảng sau thống kê chiều cao (đơn vị: cm) của một số cây giống sau khi nảy mầm được 2 tuần. Hãy ước lượng số trung bình và mốt của mẫu số liệu ghép nhóm trên.
Đề bài
Bảng sau thống kê chiều cao (đơn vị: cm) của một số cây giống sau khi nảy mầm được 2 tuần.

Hãy ước lượng số trung bình và mốt của mẫu số liệu ghép nhóm trên.
Phương pháp giải - Xem chi tiết
+ Sử dụng kiến thức về số trung bình của mẫu số liệu để tính:
Giả sử mẫu số liệu được cho dưới dạng bảng tần số ghép nhóm:
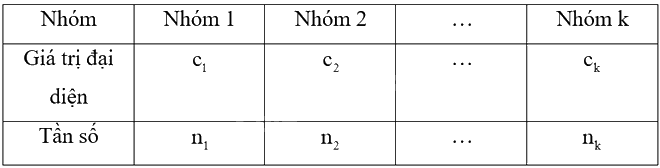
Số trung bình của mẫu số liệu ghép nhóm, kí hiệu \(\overline x \), được tính như sau: \(\overline x = \frac{{{n_1}{c_1} + {n_2}{c_2} + ... + {n_k}{c_k}}}{n}\), trong đó \(n = {n_1} + {n_2} + ... + {n_k}\).
+ Sử dụng kiến thức về mốt của mẫu số liệu để tính: Giả sử nhóm chứa mốt là \(\left[ {{u_m};{u_{m + 1}}} \right)\), khi đó mốt của mẫu số liệu ghép nhóm, kí hiệu là \({M_O}\) được xác định bởi công thức: \({M_O} = {u_m} + \frac{{{n_m} - {n_{m - 1}}}}{{\left( {{n_m} - {n_{m - 1}}} \right) + \left( {{n_m} - {n_{m + 1}}} \right)}}.\left( {{u_{m + 1}} - {u_m}} \right)\)
Lời giải chi tiết
Bảng tần số ghép nhóm bao gồm các giá trị đại diện của nhóm là:
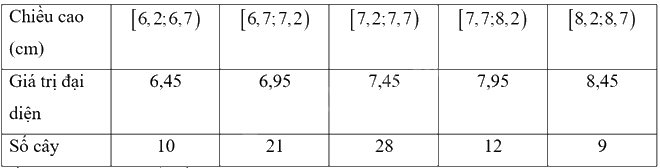
Số trung bình của mẫu số liệu ghép nhóm là:
\(\overline x = \frac{{6,45.10 + 6,95.21 + 7,45.28 + 7,95.12 + 8,45.9}}{{10 + 21 + 28 + 12 + 9}} = \frac{{1\;181}}{{160}}\)
Nhóm chứa mốt của mẫu số liệu là \(\left[ {7,2;7,7} \right)\).
Do đó, \({u_m} = 7,2;{n_{m - 1}} = 21;{n_m} = 28,{n_{m + 1}} = 12,{u_{m + 1}} - {u_m} = 7,7 - 7,2 = 0,5\)
Mốt của mẫu số liệu ghép nhóm là: \({M_O} = 7,2 + \frac{{28 - 21}}{{\left( {28 - 21} \right) + \left( {28 - 12} \right)}}.0,5 = \frac{{1\;691}}{{230}}\)
Bài 5 trang 150 sách bài tập Toán 11 - Chân trời sáng tạo tập 1 thuộc chương trình học về đạo hàm. Bài tập này thường tập trung vào việc vận dụng các quy tắc tính đạo hàm của các hàm số cơ bản như hàm đa thức, hàm lượng giác, và các phép toán trên hàm số. Việc nắm vững kiến thức về đạo hàm là nền tảng quan trọng để giải quyết các bài toán liên quan đến cực trị, khoảng đơn điệu, và ứng dụng của đạo hàm trong các lĩnh vực khác.
Bài 5 thường bao gồm các dạng bài tập sau:
Để giải bài 5 trang 150 sách bài tập Toán 11 - Chân trời sáng tạo tập 1, chúng ta cần thực hiện các bước sau:
Giả sử chúng ta có hàm số f(x) = 3x2 + 2x - 1. Để tính đạo hàm của hàm số này, chúng ta áp dụng quy tắc đạo hàm của hàm đa thức:
f'(x) = 6x + 2
Đạo hàm có rất nhiều ứng dụng trong thực tế, bao gồm:
Để học tập và ôn luyện kiến thức về đạo hàm, bạn có thể tham khảo các tài liệu sau:
Bài 5 trang 150 sách bài tập Toán 11 - Chân trời sáng tạo tập 1 là một bài tập quan trọng giúp bạn củng cố kiến thức về đạo hàm. Hy vọng rằng với hướng dẫn chi tiết và các ví dụ minh họa trong bài viết này, bạn sẽ tự tin hơn trong việc giải quyết các bài toán liên quan đến đạo hàm.