Bài 4 trang 55 sách bài tập Toán 11 Chân trời sáng tạo tập 2 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về đạo hàm và ứng dụng của đạo hàm trong việc tìm cực trị của hàm số. Bài tập này thường yêu cầu học sinh phải nắm vững các công thức đạo hàm cơ bản và các bước giải bài toán cực trị.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 4 trang 55, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Cho hình chóp S.ABCD có đáy là hình thoi, O là giao điểm của hai đường chéo, \(SA = SC,SB = SD\).
Đề bài
Cho hình chóp S.ABCD có đáy là hình thoi, O là giao điểm của hai đường chéo, \(SA = SC,SB = SD\).
a) Chứng minh rằng \(SO \bot \left( {ABCD} \right)\).
b) Gọi I, J lần lượt là trung điểm của BA, BC. Chứng minh rằng \(IJ \bot \left( {SBD} \right)\).
c) Chứng minh rằng \(BD \bot \left( {SAC} \right)\).
Phương pháp giải - Xem chi tiết
a, c) Sử dụng kiến thức về định lí đường thẳng vuông góc với mặt phẳng để chứng minh: Nếu đường thẳng d vuông góc với hai đường thẳng cắt nhau a và b cùng nằm trong mặt phẳng \(\left( \alpha \right)\) thì \(d \bot \left( \alpha \right)\).
b) Sử dụng kiến thức về liên hệ giữa tính song song và tính vuông góc của đường thẳng và mặt phẳng: Cho hai đường thẳng song song. Mặt phẳng nào vuông góc với đường thẳng này thì cũng vuông góc với đường thẳng kia.
Lời giải chi tiết
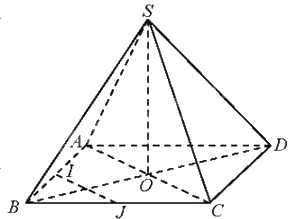
a) Vì ABCD là hình thoi tâm O nên O là trung điểm của AC, O là trung điểm của BD.
Vì \(SA = SC\) nên tam giác SAC cân tại S. Do đó, SO là đường trung tuyến đồng thời là đường cao của tam giác SAC. Do đó, \(SO \bot AC\)
Vì \(SB = SD\) nên tam giác SBD cân tại S. Do đó, SO là đường trung tuyến đồng thời là đường cao của tam giác SBD. Do đó, \(SO \bot BD\)
Vì \(SO \bot AC\), \(SO \bot BD\), AC và BD cắt nhau và nằm trong (ABCD).
Do đó, \(SO \bot \left( {ABCD} \right)\)
b) Vì \(SO \bot AC,BD \bot AC\) (do ABCD là hình thoi tâm), SO và BD cắt nhau tại O và nằm trong (SBD) nên \(AC \bot \left( {SBD} \right)\) (1)
Vì I, J lần lượt là trung điểm của BA, BC nên IJ là đường trung bình của tam giác BAC. Do đó, IJ//AC (2)
Từ (1) và (2) suy ra: \(IJ \bot \left( {SBD} \right)\).
c) Vì \(SO \bot BD,BD \bot AC\), SO và AC cắt nhau tại O và nằm trong (SAC) nên \(BD \bot \left( {SAC} \right)\).
Bài 4 trang 55 sách bài tập Toán 11 Chân trời sáng tạo tập 2 thuộc chương trình học về đạo hàm và ứng dụng của đạo hàm. Bài tập này thường tập trung vào việc tìm cực trị của hàm số, một chủ đề quan trọng trong chương trình Toán 11. Để giải bài tập này một cách hiệu quả, học sinh cần nắm vững các kiến thức sau:
(Giả sử đề bài là: Tìm cực trị của hàm số f(x) = x3 - 3x2 + 2)
f'(x) = 3x2 - 6x
3x2 - 6x = 0 ⇔ 3x(x - 2) = 0 ⇔ x = 0 hoặc x = 2
f''(x) = 6x - 6
Kết luận: Hàm số f(x) = x3 - 3x2 + 2 đạt cực đại tại x = 0 với giá trị là 2 và đạt cực tiểu tại x = 2 với giá trị là -2.
Ngoài bài 4 trang 55, sách bài tập Toán 11 Chân trời sáng tạo tập 2 còn nhiều bài tập tương tự về tìm cực trị của hàm số. Để giải các bài tập này, học sinh có thể áp dụng các bước tương tự như trên. Tuy nhiên, cần lưu ý một số điểm sau:
Để nắm vững kiến thức về tìm cực trị của hàm số, học sinh nên luyện tập thêm các bài tập khác trong sách bài tập và các tài liệu tham khảo. Giaitoan.edu.vn cung cấp nhiều bài tập luyện tập và lời giải chi tiết, giúp các em học sinh tự tin hơn trong quá trình học tập.
Hy vọng với lời giải chi tiết và những hướng dẫn trên, các em học sinh sẽ hiểu rõ hơn về cách giải bài 4 trang 55 sách bài tập Toán 11 Chân trời sáng tạo tập 2 và tự tin hơn trong quá trình học tập môn Toán.