Bài 3 trang 8 sách bài tập Toán 11 Chân trời sáng tạo tập 1 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về phép biến hóa lượng giác. Bài tập này thường yêu cầu học sinh vận dụng các công thức lượng giác cơ bản để tính toán và chứng minh các biểu thức toán học.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 3 trang 8 sách bài tập Toán 11 Chân trời sáng tạo tập 1, giúp các em học sinh nắm vững kiến thức và tự tin giải các bài tập tương tự.
Xác định số đo của các góc lượng giác được biểu diễn trong mỗi hình dưới đây. Biết trong các Hình 4a, b, c có \(\widehat {AOB} = \frac{\pi }{4}\); trong Hình 4d, e, g có \(\widehat {CID} = {82^0}\).
Đề bài
Xác định số đo của các góc lượng giác được biểu diễn trong mỗi hình dưới đây. Biết trong các Hình 4a, b, c có \(\widehat {AOB} = \frac{\pi }{4}\); trong Hình 4d, e, g có \(\widehat {CID} = {82^0}\).
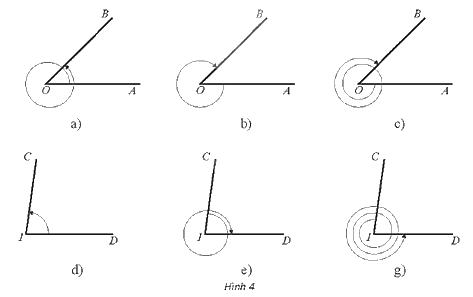
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về khái niệm góc lượng giác:
a, b, c) Số đo của các góc lượng giác có cùng tia đầu Oa và tia cuối Ob sai khác nhau một bội nguyên của \({360^0}\) nên có công thức tổng quát là: \(\left( {Oa,Ob} \right) = {\alpha ^0} + k{360^0}\left( {k \in \mathbb{Z}} \right)\) với \({\alpha ^0}\) là số đo của một góc lượng giác bất kì có tia đầu Oa và tia cuối Ob.
d, e, g) Số đo của các góc lượng giác có cùng tia đầu Oa và tia cuối Ob sai nhau khác một bội nguyên của \(2\pi \) nên ta có công thức tổng quát là \(\left( {Oa,Ob} \right) = \alpha + k2\pi \left( {k \in \mathbb{Z}} \right)\) với \(\alpha \) là số đo theo radian của một góc lượng giác bất kì có tia đầu Oa và tia cuối Ob.
Lời giải chi tiết
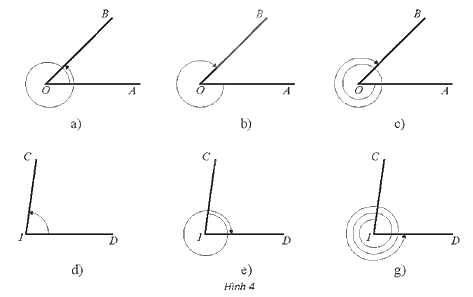
Số đo của góc lượng giác (OA, OB) trong Hình 4a là: \(\frac{\pi }{4} + 2\pi = \frac{{9\pi }}{4}\)
Số đo của góc lượng giác (OA, OB) trong Hình 4b là: \(\frac{\pi }{4} - 2\pi = - \frac{{7\pi }}{4}\)
Số đo của góc lượng giác (OA, OB) trong Hình 4c là: \(\frac{\pi }{4} - 2.2\pi = \frac{{ - 15\pi }}{4}\)
Số đo của góc lượng giác (IC, ID) trong Hình 4d là: \({82^0}\)
Số đo của góc lượng giác (IC, ID) trong Hình 4e là: \( - \left( {{{82}^0} + {{360}^0}} \right) = - {442^0}\)
Số đo của góc lượng giác (IC, ID) trong Hình 4g là: \({360^0} - {82^0} + {2.360^0} = {998^0}\)
Bài 3 trang 8 sách bài tập Toán 11 Chân trời sáng tạo tập 1 thuộc chương trình học về hàm số lượng giác và đồ thị. Bài tập này tập trung vào việc vận dụng các công thức lượng giác cơ bản, đặc biệt là các công thức biến đổi lượng giác, để đơn giản hóa biểu thức và tìm giá trị của chúng. Việc nắm vững các công thức này là nền tảng quan trọng để giải quyết bài toán và hiểu sâu hơn về hàm số lượng giác.
Bài 3 thường bao gồm các dạng bài tập sau:
Để giải bài 3 trang 8 sách bài tập Toán 11 Chân trời sáng tạo tập 1, chúng ta cần thực hiện các bước sau:
Giả sử bài tập yêu cầu rút gọn biểu thức: A = sin^2(x) + cos^2(x) + 2sin(x)cos(x)
Chúng ta có thể sử dụng công thức lượng giác cơ bản: sin^2(x) + cos^2(x) = 1 và công thức nhân đôi: 2sin(x)cos(x) = sin(2x)
Khi đó, biểu thức A được rút gọn thành: A = 1 + sin(2x)
Để học tốt môn Toán 11, bạn có thể tham khảo các tài liệu sau:
Bài 3 trang 8 sách bài tập Toán 11 Chân trời sáng tạo tập 1 là một bài tập quan trọng giúp học sinh củng cố kiến thức về hàm số lượng giác và rèn luyện kỹ năng giải toán. Hy vọng với lời giải chi tiết và các mẹo giải bài tập mà giaitoan.edu.vn cung cấp, các em học sinh sẽ tự tin hơn trong việc học tập và đạt kết quả tốt trong môn Toán.