Bài 6 trang 134 sách bài tập Toán 11 Chân trời sáng tạo tập 1 là một bài tập quan trọng giúp học sinh rèn luyện kỹ năng về tổ hợp và xác suất. Bài tập này thường yêu cầu học sinh vận dụng kiến thức đã học để giải quyết các bài toán thực tế.
Giaitoan.edu.vn xin giới thiệu lời giải chi tiết, dễ hiểu bài 6 trang 134, giúp các em học sinh hiểu rõ phương pháp giải và tự tin làm bài tập.
Cho hình chóp S. ABCD, đáy ABCD là hình thang có đáy lớn AB và \(AD = a\). Mặt bên SAB là tam giác cân tại S, \(SA = a\); mặt phẳng (R) song song với (SAB) và cắt các cạnh AD, BC, SC, SD theo thứ tự tại M, N, P, Q. a) Chứng minh MNPQ là hình thang cân. b) Đặt \(x = AM\) với \(0 < x < a\). Tính MQ theo a và x.
Đề bài
Cho hình chóp S. ABCD, đáy ABCD là hình thang có đáy lớn AB và \(AD = a\). Mặt bên SAB là tam giác cân tại S, \(SA = a\); mặt phẳng (R) song song với (SAB) và cắt các cạnh AD, BC, SC, SD theo thứ tự tại M, N, P, Q.
a) Chứng minh MNPQ là hình thang cân.
b) Đặt \(x = AM\) với \(0 < x < a\). Tính MQ theo a và x.
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về tính chất của hai mặt phẳng song song để chứng minh: Cho hai mặt phẳng (P) và (Q) song song với nhau. Nếu mặt phẳng (R) cắt (P) thì cắt (Q) và hai giao tuyến của chúng song song với nhau.
Lời giải chi tiết
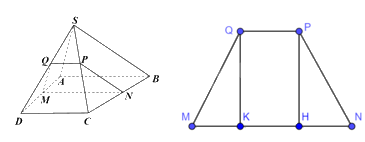
Ta có: Giao tuyến của mặt phẳng (ABCD) và (R) là MN, giao tuyến của mặt phẳng (ABCD) và (SAB) là AB. Mà (R)//(SAB) nên MN//AB.
Chứng minh tương tự ta có: các mặt phẳng (SAD), (SCB), (SCD) cắt hai mặt phẳng song song (R) và (SAB) theo các cặp giao tuyến song song.
Suy ra: MQ//SA, NP//SB, QP//CD//AB.
Do đó, MN//PQ nên tứ giác MNPQ là hình thang.
Ta có: \(\frac{{MQ}}{{SA}} = \frac{{DM}}{{DA}} = \frac{{CN}}{{CB}} = \frac{{NP}}{{SB}}\) (hệ quả định lí Thalès) và \(SA = SB \Rightarrow MQ = NP\)
Kẻ QK vuông góc với MN tại K, PH vuông góc với MN tại H.
Chứng minh được \(\Delta MKQ = \Delta NHP\left( {ch - cgv} \right) \Rightarrow \widehat {QMK} = \widehat {PNH}\)
Do đó, hình thang MNPQ là hình thang cân.
b) Ta có: \(\frac{{MQ}}{{SA}} = \frac{{DM}}{{DA}} \Rightarrow \frac{{MQ}}{a} = \frac{{a - x}}{a} \Rightarrow MQ = a - x\)
Bài 6 trong sách bài tập Toán 11 Chân trời sáng tạo tập 1 tập trung vào việc ứng dụng các kiến thức về hoán vị, chỉnh hợp và tổ hợp để giải quyết các bài toán đếm. Nắm vững các công thức và phương pháp giải là chìa khóa để hoàn thành bài tập này một cách hiệu quả.
Bài 6 thường bao gồm các dạng bài tập sau:
Để giúp các em học sinh hiểu rõ hơn về cách giải bài 6 trang 134, chúng ta sẽ đi vào phân tích từng dạng bài tập cụ thể.
Tính số hoán vị của 5 phần tử khác nhau.
Giải: Số hoán vị của 5 phần tử khác nhau là P(5) = 5! = 5 x 4 x 3 x 2 x 1 = 120.
Tính số chỉnh hợp chập 2 của 6 phần tử khác nhau.
Giải: Số chỉnh hợp chập 2 của 6 phần tử khác nhau là A(6,2) = 6! / (6-2)! = 6! / 4! = 6 x 5 = 30.
Tính số tổ hợp chập 3 của 7 phần tử khác nhau.
Giải: Số tổ hợp chập 3 của 7 phần tử khác nhau là C(7,3) = 7! / (3! x (7-3)!) = 7! / (3! x 4!) = (7 x 6 x 5) / (3 x 2 x 1) = 35.
Một lớp học có 20 học sinh, trong đó có 10 nam và 10 nữ. Cần chọn ra một ban cán sự lớp gồm 3 người, trong đó có ít nhất 1 nam và 1 nữ. Hỏi có bao nhiêu cách chọn?
Giải:
Có hai trường hợp:
Vậy tổng số cách chọn là 450 + 450 = 900 cách.
Để nắm vững kiến thức về tổ hợp và xác suất, các em có thể tham khảo thêm các tài liệu sau:
Bài 6 trang 134 sách bài tập Toán 11 Chân trời sáng tạo tập 1 là một bài tập quan trọng giúp học sinh củng cố kiến thức về tổ hợp và xác suất. Hy vọng với lời giải chi tiết và các mẹo giải bài tập trên, các em học sinh sẽ tự tin hơn khi làm bài tập và đạt kết quả tốt trong môn Toán.